
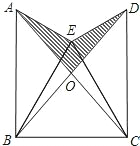
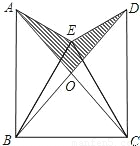
 如圖,已知△BEC是等邊三角形,∠AEB=∠DEC=90°,AE=DE,AC,BD的交點為O.
如圖,已知△BEC是等邊三角形,∠AEB=∠DEC=90°,AE=DE,AC,BD的交點為O.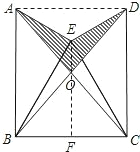 (1)證明:∵∠AEB=∠DEC=90°,
(1)證明:∵∠AEB=∠DEC=90°,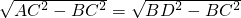 =CD,
=CD, AB=
AB= ×2=1,
×2=1,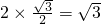 ,
,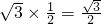 ,
,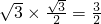 ,
,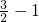 =
= ,
, •EO•BF=2×
•EO•BF=2× ×
× ×
× =
= (cm2).
(cm2). •OE•FB,所以解題中心即為求出OE和FB,有(1)中結論和已知條件即可求解.
•OE•FB,所以解題中心即為求出OE和FB,有(1)中結論和已知條件即可求解.

科目:初中數學 來源: 題型:
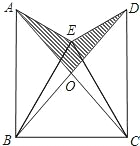 如圖,已知△BEC是等邊三角形,∠AEB=∠DEC=90°,AE=DE,AC,BD的交點為O.
如圖,已知△BEC是等邊三角形,∠AEB=∠DEC=90°,AE=DE,AC,BD的交點為O.查看答案和解析>>
科目:初中數學 來源:第1章《解直角三角形》中考題集(30):1.3 解直角三角形(解析版) 題型:解答題

查看答案和解析>>
科目:初中數學 來源:第4章《銳角三角形》中考題集(26):4.3 解直角三角形及其應用(解析版) 題型:解答題
查看答案和解析>>
科目:初中數學 來源:2006年江蘇省南通市中考數學試卷(課標卷)(解析版) 題型:解答題

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com