
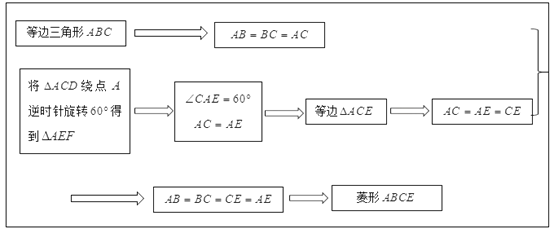
【題目】(探索發(fā)現(xiàn))
如圖,![]() 是等邊三角形,點(diǎn)
是等邊三角形,點(diǎn)![]() 為
為![]() 邊上一個動點(diǎn),將
邊上一個動點(diǎn),將![]() 繞點(diǎn)
繞點(diǎn)![]() 逆時針旋轉(zhuǎn)
逆時針旋轉(zhuǎn)![]() 得到
得到![]() ,連接
,連接![]() .小明在探索這個問題時發(fā)現(xiàn)四邊形
.小明在探索這個問題時發(fā)現(xiàn)四邊形![]() 是菱形.
是菱形.
小明是這樣想的:
(1)請參考小明的思路寫出證明過程;
(2)直接寫出線段![]() ,
,![]() ,
,![]() 之間的數(shù)量關(guān)系:______________;
之間的數(shù)量關(guān)系:______________;
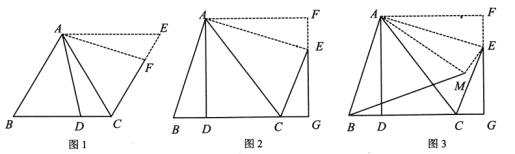
(理解運(yùn)用)
如圖,在![]() 中,
中,![]() 于點(diǎn)
于點(diǎn)![]() .將
.將![]() 繞點(diǎn)
繞點(diǎn)![]() 逆時針旋轉(zhuǎn)
逆時針旋轉(zhuǎn)![]() 得到
得到![]() ,延長
,延長![]() 與
與![]() ,交于點(diǎn)
,交于點(diǎn)![]() .
.
(3)判斷四邊形![]() 的形狀,并說明理由;
的形狀,并說明理由;
(拓展遷移)
(4)在(3)的前提下,如圖,將![]() 沿
沿![]() 折疊得到
折疊得到![]() ,連接
,連接![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的長.
的長.
【答案】(1)詳見解析;(2)![]() ;(3)四邊形
;(3)四邊形![]() 是正方形;(4)
是正方形;(4)![]()
【解析】
(1)根據(jù)旋轉(zhuǎn)得:△ACE是等邊三角形,可得:AB=BC=CE=AE,則四邊形ABCE是菱形;
(2)先證明C、F、E在同一直線上,再證明△BAD≌△CAF(SAS),則∠ADB=∠AFC,BD=CF,可得AC=CF+CD;
(3)先根據(jù)∠ADC=∠DAF=∠F=90°,證明得四邊形ADGF是矩形,由鄰邊相等可得四邊形ADGF是正方形;
(4)證明△BAM≌△EAD(SAS),根據(jù)BM=DE及勾股定理可得結(jié)論.
(1)證明:∵![]() 是等邊三角形,
是等邊三角形,
∴![]() .
.
∵![]() 繞點(diǎn)
繞點(diǎn)![]() 逆時針旋轉(zhuǎn)
逆時針旋轉(zhuǎn)![]() 得到
得到![]() ,
,
∴![]() ,
,![]() .
.
∴![]() 是等邊三角形.
是等邊三角形.
∴![]() .
.
∴![]() .
.
∴四邊形![]() 是菱形.
是菱形.
(2)線段![]() ,
,![]() ,
,![]() 之間的數(shù)量關(guān)系:
之間的數(shù)量關(guān)系:![]() .
.
(3)四邊形![]() 是正方形.理由如下:
是正方形.理由如下:
∵![]() 繞點(diǎn)
繞點(diǎn)![]() 逆時針旋轉(zhuǎn)
逆時針旋轉(zhuǎn)![]() 得到
得到![]() ,
,
∴![]() ,
,![]() .
.
∵![]() ,
,
∴![]() .
.
∴四邊形![]() 是矩形.
是矩形.
∵![]() ,
,
∴四邊形![]() 是正方形.
是正方形.
(4)如圖,連接![]() .
.
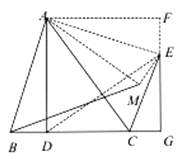
∵四邊形![]() 是正方形,
是正方形,
∴![]() .
.
∵![]() 繞點(diǎn)
繞點(diǎn)![]() 逆時針旋轉(zhuǎn)
逆時針旋轉(zhuǎn)![]() 得到
得到![]() ,
,
∴![]() ,
,![]() ,∴
,∴![]() .
.
∵將![]() 沿
沿![]() 折疊得到
折疊得到![]() ,
,
∴![]() ,
,![]() .
.
∴![]() .
.
∴![]() ,即
,即![]() .
.
∵![]() ,
,
∴![]() .
.
在![]() 和
和![]() 中,
中,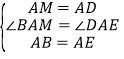 ,
,
∴![]() .
.
∴![]() .
.


 閱讀快車系列答案
閱讀快車系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,若干個全等的正五邊形排成環(huán)狀,圖中所示的是前3個正五邊形,要完成這一圓環(huán)還需正五邊形的個數(shù)為( )
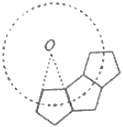
A. 10 B. 9 C. 8 D. 7
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
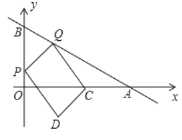
【題目】如圖,在平面直角坐標(biāo)系中,直線![]() 與
與![]() 軸、
軸、![]() 軸分別角與A、B兩點(diǎn),P、Q分別是線段OB、AB上的兩個動點(diǎn),點(diǎn)P從O出發(fā)一每秒2個單位長度的速度向終點(diǎn)B運(yùn)動,同時Q從B出發(fā),以每秒5個單位的速度向終點(diǎn)A運(yùn)動,當(dāng)其中一點(diǎn)到達(dá)終點(diǎn)時整個運(yùn)動結(jié)束,設(shè)運(yùn)動時間為t秒。
軸分別角與A、B兩點(diǎn),P、Q分別是線段OB、AB上的兩個動點(diǎn),點(diǎn)P從O出發(fā)一每秒2個單位長度的速度向終點(diǎn)B運(yùn)動,同時Q從B出發(fā),以每秒5個單位的速度向終點(diǎn)A運(yùn)動,當(dāng)其中一點(diǎn)到達(dá)終點(diǎn)時整個運(yùn)動結(jié)束,設(shè)運(yùn)動時間為t秒。
(1)求出點(diǎn)Q的坐標(biāo)(用t的代數(shù)式表示)
(2)若C為OA的中點(diǎn),連接PQ、CQ,以PQ、CQ為鄰邊作![]() PQCD.
PQCD.
①是否存在時間t,使得坐標(biāo)軸切好將![]() PQCD的面積分為1:5的兩個部分,若存在,求出t的值;若不存在,請說明理由.
PQCD的面積分為1:5的兩個部分,若存在,求出t的值;若不存在,請說明理由.
②直接寫出整個運(yùn)動過程中![]() PQCD對角線DQ的取值范圍.
PQCD對角線DQ的取值范圍.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,已知△AOB和△A1OB1是以點(diǎn)O為位似中心的位似圖形,且△AOB和△A1OB1的周長之比為1:2,點(diǎn)B的坐標(biāo)為(-1,2),則點(diǎn)B1的坐標(biāo)為( )
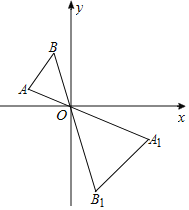
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】(問題)如圖①,在a×b×c(長×寬×高,其中a,b,c為正整數(shù))個小立方塊組成的長方體中,長方體的個數(shù)是多少?
(探究)

探究一:
(1)如圖②,在2×1×1個小立方塊組成的長方體中,棱AB上共有1+2=![]() =3條線段,棱AC,AD上分別只有1條線段,則圖中長方體的個數(shù)為3×1×1=3.
=3條線段,棱AC,AD上分別只有1條線段,則圖中長方體的個數(shù)為3×1×1=3.
(2)如圖③,在3×1×1個小立方塊組成的長方體中,棱AB上共有1+2+3=![]() =6條線段,棱AC,AD上分別只有1條線段,則圖中長方體的個數(shù)為6×1×1=6.
=6條線段,棱AC,AD上分別只有1條線段,則圖中長方體的個數(shù)為6×1×1=6.
(3)依此類推,如圖④,在a×1×1個小立方塊組成的長方體中,棱AB上共有1+2+…+a=![]() 線段,棱AC,AD上分別只有1條線段,則圖中長方體的個數(shù)為______.
線段,棱AC,AD上分別只有1條線段,則圖中長方體的個數(shù)為______.
探究二:
(4)如圖⑤,在a×2×1個小立方塊組成的長方體中,棱AB上有![]() 條線段,棱AC上有1+2=
條線段,棱AC上有1+2=![]() =3條線段,棱AD上只有1條線段,則圖中長方體的個數(shù)為
=3條線段,棱AD上只有1條線段,則圖中長方體的個數(shù)為![]() ×3×1=
×3×1=![]() .
.
(5)如圖⑥,在a×3×1個小立方塊組成的長方體中,棱AB上有![]() 條線段,棱AC上有1+2+3=
條線段,棱AC上有1+2+3=![]() =6條線段,棱AD上只有1條線段,則圖中長方體的個數(shù)為______.
=6條線段,棱AD上只有1條線段,則圖中長方體的個數(shù)為______.
(6)依此類推,如圖⑦,在a×b×1個小立方塊組成的長方體中,長方體的個數(shù)為______.
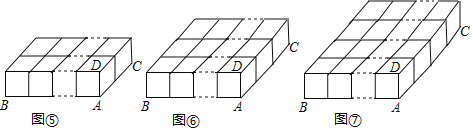
探究三:
(7)如圖⑧,在以a×b×2個小立方塊組成的長方體中,棱AB上有![]() 條線段,棱AC上有
條線段,棱AC上有![]()
條線段,棱AD上有1+2=![]() =3條線段,則圖中長方體的個數(shù)為
=3條線段,則圖中長方體的個數(shù)為![]() ×
×![]() ×3=
×3=![]() .
.
(8)如圖⑨,在a×b×3個小立方塊組成的長方體中,棱AB上有![]() 條線段,棱AC上有
條線段,棱AC上有![]() 條線段,棱AD上有1+2+3=
條線段,棱AD上有1+2+3=![]() =6條線段,則圖中長方體的個數(shù)為______.
=6條線段,則圖中長方體的個數(shù)為______.
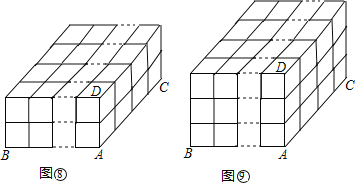
(結(jié)論)如圖①,在a×b×c個小立方塊組成的長方體中,長方體的個數(shù)為______.
(應(yīng)用)在2×3×4個小立方塊組成的長方體中,長方體的個數(shù)為______.
(拓展)
如果在若干個小立方塊組成的正方體中共有1000個長方體,那么組成這個正方體的小立方塊的個數(shù)是多少?請通過計算說明你的結(jié)論.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】某小學(xué)學(xué)生較多,為了便于學(xué)生盡快就餐,師生約定:早餐一人一份,一份兩樣,一樣一個,食堂師傅在窗口隨機(jī)發(fā)放(發(fā)放的食品價格一樣),食堂在某天早餐提供了豬肉包、面包、雞蛋、油餅四樣食品.
(1)按約定,“小李同學(xué)在該天早餐得到兩個油餅”是 事件;(可能,必然,不可能)
(2)請用列表或樹狀圖的方法,求出小張同學(xué)該天早餐剛好得到豬肉包和油餅的概率.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
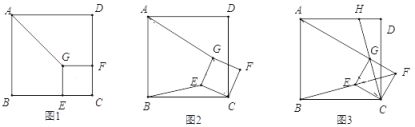
【題目】已知:正方形![]() 與正方形
與正方形![]() 共頂點(diǎn)
共頂點(diǎn)![]() .
.
(1)探究:如圖,點(diǎn)![]() 在正方形
在正方形![]() 的邊
的邊![]() 上,點(diǎn)
上,點(diǎn)![]() 在正方形
在正方形![]() 的邊
的邊![]() 上,連接
上,連接![]() .求證:
.求證:![]() ;
;
(2)拓展:將如圖中正方形![]() 繞點(diǎn)
繞點(diǎn)![]() 順時針方向旋轉(zhuǎn)
順時針方向旋轉(zhuǎn)![]() 角
角![]() ,如圖所示,試探究線段
,如圖所示,試探究線段![]() 與
與![]() 之間的數(shù)量關(guān)系,并說明理由;
之間的數(shù)量關(guān)系,并說明理由;
(3)運(yùn)用:正方形![]() 在旋轉(zhuǎn)過程中,當(dāng)
在旋轉(zhuǎn)過程中,當(dāng)![]() ,
,![]() ,
,![]() 三點(diǎn)在一條直線上時,如圖所示,延長
三點(diǎn)在一條直線上時,如圖所示,延長![]() 交
交![]() 于點(diǎn)
于點(diǎn)![]() .若
.若![]() ,GH=2
,GH=2![]() ,求
,求![]() 的長.
的長.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
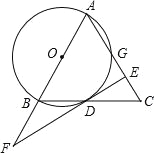
【題目】如圖,在△ABC中,AB=AC,以AB為直徑作⊙O,交BC邊于邊D,交AC邊于點(diǎn)G,過D作⊙O的切線EF,交AB的延長線于點(diǎn)F,交AC于點(diǎn)E.
(1)求證:BD=CD;
(2)若AE=6,BF=4,求⊙O的半徑.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】二次函數(shù)y=ax2+bx+c(a≠0)的圖象如圖,給出下列四個結(jié)論:①4ac﹣b2<0;②4a+c<2b;③3b+2c<0;④m(am+b)+b<a(m≠﹣1),其中正確結(jié)論的個數(shù)是( )
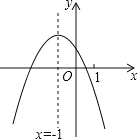
A.4個B.3個C.2個D.1個
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com