
【題目】某同學所在年級的500名學生參加志愿者活動,現有以下5個志愿服務項目:A,紀念館志講解員.B.書香社區圖書整理C.學編中國結及義賣.D,家風講解員E.校內志愿服務,要求:每位學生都從中選擇一個項目參加,為了了解同學們選擇這個5個項目的情況,該同學隨機對年級中的40名同學選擇的志愿服務項目進行了調查,過程如下:
收集數據:設計調查問卷,收集到如下數據(志愿服務項目的編號,用字母代號表示)
B,E,B,A,E,C,C,C,B,B,
A,C,E,D,B,A,B,E,C,A,
D,D,B,B,C,C,A,E,B
C,B,D,C,A,C,C,A,C,E,
(1)整理、描述詩句:劃記、整理、描述樣本數據,繪制統計圖如下,請補全統計表和統計圖

選擇各志愿服務項目的人數統計表
志愿服務項目 | 劃記 | 人數 |
A.紀念館志愿講解員 | 正 | 8 |
B.書香社區圖書整理 | ||
C.學編中國結及義賣 | 正正 | 12 |
D.家風講解員 | ||
E.校內志愿服務 | 正 一 | 6 |
合計 | 40 | 40 |
分析數據、推斷結論
(2)抽樣的40個樣本數據(志愿服務項目的編號)的眾數是 (填A﹣E的字母代號)
(3)請你任選A﹣E中的兩個志愿服務項目,根據該同學的樣本數據估計全年級大約有多少名同學選擇這兩個志愿服務項目.
【答案】(1)B占25%,D占10%.(2)C(3)A:500×20%=100(人).B:500×25%=125(人).C:500×30%=150(人).D:500×10%=50(人).E:500×15%=75(人).
【解析】
依據收集的數據,即可得到補全統計表和統計圖;依據抽樣的40個樣本數據(志愿服務項目的編號)中,C出現的次數最多,可得眾數是C.依據A-E中的各志愿服務項目在樣本中所占的百分比,即可得到全年級大約有多少名同學選擇某兩個志愿服務項目.
整理、描述數據:
(1)由題可得,A項有8人,B項有10人,D項有4人.
選擇各志愿服務項目的人數比例統計圖中,B占10÷40=25%,D占4÷40=10%.
分析數據、推斷結論:
(2)抽樣的40個樣本數據(志愿服務項目的編號)中,C出現的次數最多,故眾數是C.
故答案為:C.
(3)(寫出任意兩個即可).A:500×20%=100(人).B:500×25%=125(人).C:500×30%=150(人).D:500×10%=50(人).E:500×15%=75(人).


科目:初中數學 來源: 題型:
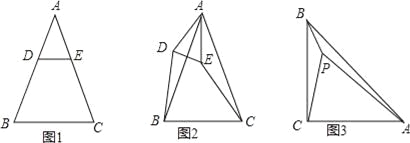
【題目】已知△ABC是等腰三角形,AB=AC.
(1)特殊情形:如圖1,當DE∥BC時,有DB EC.(填“>”,“<”或“=”)
(2)發現探究:若將圖1中的△ADE繞點A順時針旋轉α(0°<α<180°)到圖2位置,則(1)中的結論還成立嗎?若成立,請給予證明;若不成立,請說明理由.
(3)拓展運用:如圖3,P是等腰直角三角形ABC內一點,∠ACB=90°,且PB=1,PC=2,PA=3,求∠BPC的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我們把具有一條公共邊的兩個三角形稱為“友鄰三角形”,兩個三角形的公共邊所對的頂點稱為“友鄰頂點”.
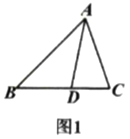
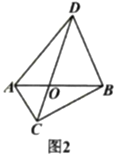
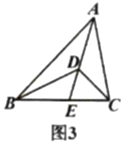
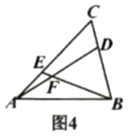
(1)如圖1,寫出圖中所有的“友鄰三角形”;
(2)如圖2,![]() 與
與![]() 相交于點
相交于點![]() ,記
,記![]() 的面積為
的面積為![]() ,
,![]() 的面積為
的面積為![]() ,求證:
,求證:![]() ;
;
(3)從圖3中找出兩對“友鄰三角形”,探索是否存在(2)中類似的結論,并直接寫出結果;
(4)如圖4,![]() ,
,![]() ,若
,若![]() 的面積為21,求
的面積為21,求![]() 的面積.
的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
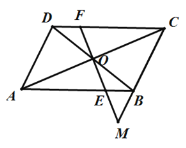
【題目】如圖,ABCD的對角線AC,BD相交于點O,EF經過點O,分別交AB,CD于點E,F,FE的延長線交CB的延長線于點M.
(1)求證:OE=OF;
(2)若AD=4,AB=6,BM=1,求BE的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知二次函數y=(a﹣1)x2+3ax+1圖象上的四個點的坐標為(x1,m),(x2,m),(x3,n),(x4,n),其中m<n.下列結論可能正確的是( )
A.若a>![]() ,則 x1<x2<x3<x4
,則 x1<x2<x3<x4
B.若a>![]() ,則 x4<x1<x2<x3
,則 x4<x1<x2<x3
C.若a<﹣![]() ,則 x1<x3<x2<x4
,則 x1<x3<x2<x4
D.若a<﹣![]() ,則 x3<x2<x1<x4
,則 x3<x2<x1<x4
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系xOy中,過⊙T外一點P引它的兩條切線,切點分別為M,N,若![]() ,則稱P為⊙T的環繞點.
,則稱P為⊙T的環繞點.
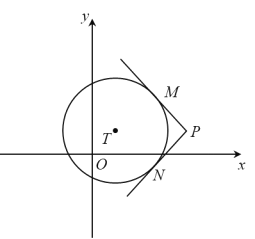
(1)當⊙O半徑為1時,
①在![]() 中,⊙O的環繞點是___________;
中,⊙O的環繞點是___________;
②直線y=2x+b與x軸交于點A,y軸交于點B,若線段AB上存在⊙O的環繞點,求b的取值范圍;
(2)⊙T的半徑為1,圓心為(0,t),以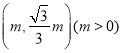 為圓心,
為圓心,![]() 為半徑的所有圓構成圖形H,若在圖形H上存在⊙T的環繞點,直接寫出t的取值范圍.
為半徑的所有圓構成圖形H,若在圖形H上存在⊙T的環繞點,直接寫出t的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線![]() 與
與![]() 軸交于
軸交于![]() 、
、![]() 兩點,與
兩點,與![]() 軸交于點
軸交于點![]() ,
,![]() .
.

(1)求拋物線的解析式;
(2)點![]() 為第一象限拋物線上一點,連接
為第一象限拋物線上一點,連接![]() 、
、![]() ,設點
,設點![]() 的橫坐標為
的橫坐標為![]() ,
,![]() 的面積為
的面積為![]() ,求
,求![]() 與
與![]() 的函數關系式;
的函數關系式;
(3)在(2)的條件下,點![]() 為第四象限拋物線上一點,連接
為第四象限拋物線上一點,連接![]() ,過點
,過點![]() 作
作![]() 軸的垂線交
軸的垂線交![]() 于點
于點![]() ,射線
,射線![]() 交第三象限拋物線于點
交第三象限拋物線于點![]() ,連接
,連接![]() ,若
,若![]() ,
,![]() ,求點
,求點![]() 的坐標.
的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
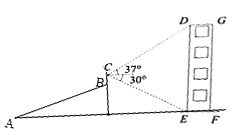
【題目】某同學利用數學知識測量建筑物DEFG的高度.他從點![]() 出發沿著坡度為
出發沿著坡度為![]() 的斜坡AB步行26米到達點B處,用測角儀測得建筑物頂端
的斜坡AB步行26米到達點B處,用測角儀測得建筑物頂端![]() 的仰角為37°,建筑物底端
的仰角為37°,建筑物底端![]() 的俯角為30°,若AF為水平的地面,側角儀豎直放置,其高度BC=1.6米,則此建筑物的高度DE約為(精確到
的俯角為30°,若AF為水平的地面,側角儀豎直放置,其高度BC=1.6米,則此建筑物的高度DE約為(精確到![]() 米,參考數據:
米,參考數據:![]() ,
,![]() )( )
)( )
A.![]() 米B.
米B.![]() 米C.
米C.![]() 米D.
米D.![]() 米
米
查看答案和解析>>
科目:初中數學 來源: 題型:
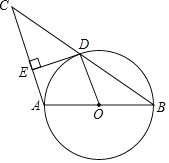
【題目】如圖,以△ABC的邊AB為直徑的⊙O恰好過BC的中點D,過點D作DE⊥AC于E,連結OD,則下列結論中:①OD∥AC;②∠B=∠C;③2OA=BC;④DE是⊙O的切線;⑤∠EDA=∠B,正確的序號是_____.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com