【題目】若△ABC≌△MNP，∠A=∠M，∠C=∠P，AB=4cm，BC=2cm，則 NP=（ ）
A. 2cm B. 3cm C. 4cm D. 6cm
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦！ | 初一 | 初一免費(fèi)課程推薦！ |
| 高二 | 高二免費(fèi)課程推薦！ | 初二 | 初二免費(fèi)課程推薦！ |
| 高三 | 高三免費(fèi)課程推薦！ | 初三 | 初三免費(fèi)課程推薦！ |
科目：初中數(shù)學(xué) 來源： 題型：
【題目】為備戰(zhàn)2011年4月11日在紹興舉行的第三屆全國皮劃艇馬拉松賽，甲、乙運(yùn)動員進(jìn)行了艱苦的訓(xùn)練，他們在相同條件下各10次劃艇成績的平均數(shù)相同，方差分別為0.23，0.20，則成績較為穩(wěn)定的是_________．（選填“甲”或“乙）
查看答案和解析>>
科目：初中數(shù)學(xué) 來源： 題型：
【題目】把（+5）﹣（+3）﹣（﹣1）+（﹣4）寫成省略括號的和的形式是（ ）
A.﹣5﹣3+1﹣4
B.5﹣3﹣1﹣4
C.5﹣3+1﹣4
D.5+3+1﹣4
查看答案和解析>>
科目：初中數(shù)學(xué) 來源： 題型：
【題目】“兩條直線相交只有一個交點(diǎn)”的題設(shè)是（ ）
A. 兩條直線 B. 相交
C. 只有一個交點(diǎn) D. 兩條直線相交
查看答案和解析>>
科目：初中數(shù)學(xué) 來源： 題型：
【題目】如右圖，在△ABC中，點(diǎn)Q，P分別是邊AC，BC上的點(diǎn)，AQ=PQ，PR⊥AB于R，PS⊥AC于S，且PR=PS，下面四個結(jié)論：①AP平分∠BAC；②AS=AR；③BP=QP；④QP∥AB．其中一定正確的是( )
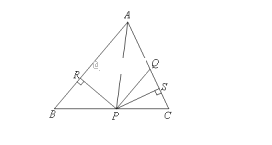
A. ①②③ B. ①③④ C. ①②④ D. ②③④
查看答案和解析>>
科目：初中數(shù)學(xué) 來源： 題型：
【題目】如圖，∠BAD=∠CAE=90o，AB=AD，AE=AC， AF⊥CF，垂足為F.
（1）若AC=10，求四邊形ABCD的面積；
（2）求證：AC平分∠ECF；
（3）求證：CE=2AF .
查看答案和解析>>
科目：初中數(shù)學(xué) 來源： 題型：
【題目】請仔細(xì)閱讀下面材料，然后解決問題：
在分式中，對于只含有一個字母的分式，當(dāng)分子的次數(shù)大于或等于分母的次數(shù)時，我們稱之為“假分式”．例如： 
， 
；當(dāng)分子的次數(shù)小于分母的次數(shù)時，我們稱之為“真分式”，例如： 
， 
．我們知道，假分?jǐn)?shù)可以化為帶分?jǐn)?shù)，例如： 
，類似的，假分式也可以化為“帶分式”（整式與真分式和的形式），例如： 
．
（1）將分式
化為帶分式；
（2）當(dāng)x取哪些整數(shù)值時，分式
的值也是整數(shù)？
（3）當(dāng)x的值變化時，分式
的最大值為 ．
【答案】（1）2+
；（2）x=0，2，﹣2，4；（3）
.
【解析】試題分析：（1）仿照閱讀材料中的方法加你個原式變形即可；
（2）原式變形后，根據(jù)結(jié)果為整數(shù)確定出整數(shù)x的值即可；
（3）原式變形后，確定出分式的最大值即可．
試題解析:（1）原式=
=2+
；
（2）由（1）得： 
=2+
，
要使
為整數(shù)，則
必為整數(shù)，
∴x﹣1為3的因數(shù)，
∴x﹣1=±1或±3，
解得：x=0，2，﹣2，4；
（3）原式=
=2+
，
當(dāng)x2=0時，原式取得最大值
．
故答案為： 
.
【題型】解答題
【結(jié)束】
28
【題目】已知，△ABC中,AC＝BC,∠ACB＝90°，點(diǎn)P在射線AC上,連接PB,將線段PB繞點(diǎn)B逆時針旋轉(zhuǎn)90°得線段BN，AN交直線BC于M．
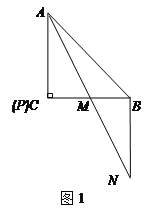
(1)圖1，若點(diǎn)P與點(diǎn)C重合，則
＝______,
＝______．(直接寫出結(jié)果)
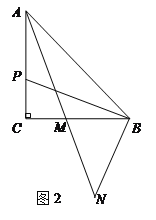
(2)圖2，若點(diǎn)P在線段AC上，求證: AP＝2MC；
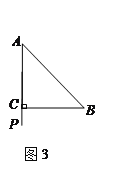
(3)圖3，若點(diǎn)P在線段AC的延長線上，完成圖形,并直接寫出
＝______．
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com