【題目】解方程
（1）x2+1＝3x
（2）（x﹣2）（x﹣3）＝12
（3）（2x﹣3）2+x（2x﹣3）＝0（因式分解法）
（4）2x2﹣4x﹣1＝0（用配方法）．
【答案】（1）x1
，x2＝
；（2）x1＝6或x2＝﹣1；（3）x1＝
，x2＝1；（4）x1＝1+
，x2＝1﹣．
【解析】
（1）根據公式法即可求解；
（2）先化簡，再根據因式分解法求解；
（3）根據因式分解法求解；
（4）根據配方法即可求解.
（1）x2﹣3x+1＝0∵a＝1，b＝﹣3，c＝1，
∴△＝b2﹣4ac＝（﹣3）2﹣4×1×1＝5＞0，
∴x＝
＝
，
即x1，x2＝．
（2）原方程整理為x2﹣5x﹣6＝0，
∵（x﹣6）（x+1）＝0，
∴x﹣6＝0或x+1＝0，
則x1＝6或x2＝﹣1．
（3）（2x﹣3）（2x﹣3+x）＝0，
2x﹣3＝0或2x﹣3+x＝0，
所以x1＝，x2＝1；
（4））x2﹣2x＝
，
x2﹣2x+1＝+1，
（x﹣1）2＝，x﹣1＝±，
所以x1＝1+，x2＝1﹣．
輕松課堂單元期中期末專題沖刺100分系列答案科目：初中數學 來源： 題型：
【題目】有一個二次函數滿足以下條件：
①函數圖象與x軸的交點坐標分別為A（1，0），B（x2，y2）（點B在點A的右側）；
②對稱軸是x=3；
③該函數有最小值是﹣2．
（1）請根據以上信息求出二次函數表達式；
（2）將該函數圖象x＞x2的部分圖象向下翻折與原圖象未翻折的部分組成圖象“G”，平行于x軸的直線與圖象“G”相交于點C（x3，y3）、D（x4，y4）、E（x5，y5）（x3＜x4＜x5），結合畫出的函數圖象求x3+x4+x5的取值范圍．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知二次函數
．
（1）求出該函數圖象的頂點坐標，對稱軸，圖象與
軸、
軸的交點坐標；
（2）在什么范圍內時，隨的增大而增大？當在什么范圍內時，隨的增大而減小？
（3）當在什么范圍內時，
？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，正方形ABCD中，點E是AD邊的中點，BD，CE交于點H，BE、AH交于點G，則下列結論：①∠ABE＝∠DCE；②AG⊥BE；③S△BHE＝S△CHD；④∠AHB＝∠EHD．其中正確的是（ ）
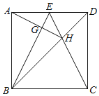
A.①③B.①②③④C.①②③D.①③④
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知函數y=﹣
（x+1）2﹣2
（1）指出函數圖象的開口方向是 ，對稱軸是 ，頂點坐標為
（2）當x 時，y隨x的增大而增大
（3）怎樣移動拋物線y=﹣x2就可以得到拋物線y=﹣（x+1）2﹣2
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖,二次函數的圖象與x軸相交于A(3,0)、B(1,0)兩點,與y軸相交于點C(0,3)，點C.D是二次函數圖象上的一對對稱點，一次函數的圖象過點B. D.
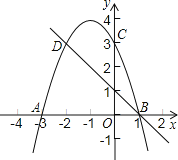
(1)求D點坐標；
(2)根據圖象直接寫出使一次函數值小于二次函數值的x的取值范圍
(3)求二次函數的解析式及頂點坐標；
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知二次函數y＝ax2+bx+c（a＜0，b，c為常數）的圖象如圖所示，下列5個結論：①abc＜0；②b＜a+c；③4a+2b+c＞0；④3b＞2c；⑤a+b＞m（am+b）（m為常數，且m≠1），其中正確的結論有_____．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】小明家客廳里裝有一種三位單極開關，分別控制著A（樓梯）、B（客廳）、C（走廊）三盞電燈，按下任意一個開關均可打開對應的一盞電燈，因剛搬進新房不久，不熟悉情況．
（1）若小明任意按下一個開關，則下列說法正確的是 ．
A．小明打開的一定是樓梯燈
B．小明打開的可能是臥室燈
C．小明打開的不可能是客廳燈
D．小明打開走廊燈的概率是
（2）若任意按下一個開關后，再按下另兩個開關中的一個，則正好客廳燈和走廊燈同時亮的概率是多少？請用樹狀圖法或列表法加以說明．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
