【題目】在有些情況下，不需要計算出結果也能把絕對值符號去掉．例如：|6+7|＝6+7；|6﹣7|＝7﹣6；|7﹣6|＝7﹣6；|﹣6﹣7|＝6+7
（1）根據上面的規律，把下列各式寫成去掉絕對值符號的形式：
①|7﹣21|＝ ；②|﹣
﹣0.8|＝ ；③|
﹣
|＝ ：
（2）數a在數軸上的位置如圖所示，則|a﹣2.5|＝ ．
A．a﹣2.5
B.2.5﹣a
C．a+2.5
D．﹣a﹣2.5
（3）利用上述介紹的方法計算或化簡：
①|
﹣
|+|﹣|﹣|﹣|+
；
②|﹣
|+|﹣|﹣|﹣|+2（），其中a＞2．
【答案】（1）①21﹣7；②
+0.8；③
﹣
；（2）B；（3）①
；②當2＜a＜5時，
；當a≥5時，
【解析】
（1）首先根據有理數的運算法則判斷式子的符號，再根據絕對值的性質正確化簡；
（2）根據數軸上a的位置判斷式子的符號，再根據絕對值的性質正確化簡；
（3）①根據分子相等時，分母大的值越小，可判定式子的符號，再根據絕對值的性質正確化簡；②分情況討論并化簡．
解：（1）①|7﹣21|＝21﹣7；②|﹣﹣0.8|＝
；③|﹣|＝﹣；
故答案為：①21﹣7；②+0.8；③﹣；
（2）由數軸得：a＜2.5，
則|a﹣2.5|＝2.5﹣a，
故選：B；
（3）利用上述介紹的方法計算或化簡：
①|﹣
|+|﹣|﹣|﹣|+
；
＝
+
﹣+，
＝﹣
，
＝，
②|﹣
|+|﹣|﹣|﹣|+2（），其中a＞2．
當2＜a＜5時，原式＝﹣+﹣﹣+
，
＝﹣
，
＝，
當a≥5時，原式＝
+﹣﹣+，
＝．
教材全解字詞句篇系列答案科目：初中數學 來源： 題型：
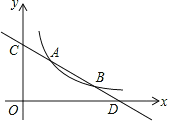
【題目】直線y=kx+b與反比例函數y=
（x＞0）的圖象分別交于點 A（m，3）和點B（6，n），與坐標軸分別交于點C和點D．
（1）求直線AB的解析式；
（2）若點P是x軸上一動點，當△COD與△ADP相似時，求點P的坐標．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】將邊長OA=8，OC=10的矩形OABC放在平面直角坐標系中，頂點O為原點，頂點C、A分別在
軸和y軸上.在OA邊上選取適當的點E，連接CE，將△EOC沿CE折疊。
（1）如圖①，當點O落在AB邊上的點D處時，點E的坐標為 ；
（2）如圖②，當點O落在矩形OABC內部的點D處時，過點E作EG∥軸交CD于點H，交BC于點G.求證：EH＝CH；
（3）在（2）的條件下，設H（m，n），寫出m與n之間的關系式 ；
（4）如圖③，將矩形OABC變為正方形，OC＝10，當點E為AO中點時，點O落在正方形OABC內部的點D處，延長CD交AB于點T，求此時AT的長度。
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某網店銷售甲、乙兩種羽毛球，已知甲種羽毛球每筒的售價比乙種羽毛球多15元，王老師從該網店購買了2筒甲種羽毛球和3筒乙種羽毛球，共花費255元．
（1）該網店甲、乙兩種羽毛球每筒的售價各是多少元？
（2）根據消費者需求，該網店決定用不超過8780元購進甲、乙兩種羽毛球共200筒，且甲種羽毛球的數量大于乙種羽毛球數量的
，已知甲種羽毛球每筒的進價為50元，乙種羽毛球每筒的進價為40元．
①若設購進甲種羽毛球m筒，則該網店有哪幾種進貨方案？
②若所購進羽毛球均可全部售出，請求出網店所獲利潤W（元）與甲種羽毛球進貨量m（筒）之間的函數關系式，并說明當m為何值時所獲利潤最大？最大利潤是多少？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】同學報名次參加學校秋季運動會，有以下5個項目可供選擇：徑賽項目：100m、200m、1000m（分別用A1、A2、A3表示）；田賽項目：跳遠，跳高（分別用T1、T2表示）
（1）該同學從5個項目中任選一個，恰好是田賽項目的概率P為___________；
（2）該同學從5個項目中任選兩個，求恰好是一個徑賽項目和一個田賽項目的概率P1，利用列表法或樹狀圖加以說明；
（3）該同學從5個項目中任選兩個，則兩個項目都是徑賽項目的概率P2為___________.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，四邊形ACDE是證明勾股定理時用到的一個圖形，a、b、c是Rt△ABC和Rt△BED邊長，易知AE=
c，這時我們把關于x的形如ax+
cx+b=0的一元二次方程稱為“勾系一元二次方程”.
請解決下列問題：
寫出一個“勾系一元二次方程”；
求證：關于x的“勾系一元二次方程”ax+
cx+b=0必有實數根；
若x=1是“勾系一元二次方程”ax+
cx+b=0的一個根，且四邊形ACDE的周長是
，求△ABC面積.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】(12分)如圖，在Rt△ABC中，∠ACB＝90°，AC＝8，BC＝6，CD⊥AB于點D.點P從點D出發，沿線段DC向點C運動，點Q從點C出發，沿線段CA向點A運動，兩點同時出發，速度都為每秒1個單位長度，當點P運動到C時，兩點都停止．設運動時間為t秒．
(1)求線段CD的長；
(2)設△CPQ的面積為S，求S與t之間的函數關系式，并確定在運動過程中是否存在某一時刻t，使得S△CPQ∶S△ABC＝9∶100？若存在，求出t的值；若不存在，說明理由；
(3)當t為何值時，△CPQ為等腰三角形？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，兩條直線AB,CD相交于點O，且
，射線OM從OB開始繞O點逆時針方向旋轉，速度為
，射線ON同時從OD開始繞O點順時針方向旋轉，速度為
.兩條射線OM、ON同時運動，運動時間為t秒.（本題出現的角均小于平角）
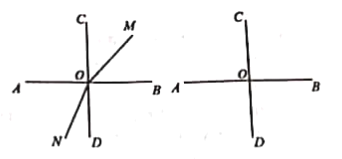
（1）當
時，若
.試求出的值；
（2）當
時，探究
的值，問：t滿足怎樣的條件是定值；滿足怎樣的條件不是定值？
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
