
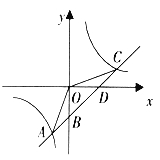
【題目】如圖,已知一次函數![]() 的圖象與反比例函數
的圖象與反比例函數![]() 的圖象的兩個交點是A(-2,-4),C(4,n),與y軸交于點B,與x軸交于點D.
的圖象的兩個交點是A(-2,-4),C(4,n),與y軸交于點B,與x軸交于點D.
(1)求反比例函數![]() 和一次函數
和一次函數![]() 的解析式;
的解析式;
(2)連結OA,OC,求△AOC的面積.
【答案】(1)![]() ;(2)6.
;(2)6.
【解析】試題分析:(1)直接把A點代入反比例函數的解析式求出m的值即可求出其解析式;再根據點C在反比例函數的圖象上把點C的坐標代入反比例函數的解析式即可求出n的值,把A、C的坐標代入一次函數關系式即可求出一次函數的解析式;
(2)根據B是直線AC與y軸的交點求出B點坐標,再由S△AOC=S△AOB+S△COB進行計算即可.
解:(1)∵A(﹣2,﹣4)在函數![]() 的圖象上,∴m=8,∴反比例函數的解析式為:
的圖象上,∴m=8,∴反比例函數的解析式為: ![]() .
.
∵點C(4,n)在函數![]() 的圖象上,∴n=2,即C(4,2),
的圖象上,∴n=2,即C(4,2),
∵![]() 經過A(﹣2,﹣4),C(4,2),
經過A(﹣2,﹣4),C(4,2),
∴![]() ,解得
,解得![]() ,
,
∴一次函數的解析式為: ![]() ;
;
(2)∵B是直線AC與y軸的交點,∴當x=0時,y=﹣2,
∴點B(0,﹣2),即OB=2,∴S△AOC=S△AOB+S△COB=![]() =6.
=6.


科目:初中數學 來源: 題型:
【題目】我國政府從2007年起對職業中專在校生給予生活補貼,每位在校生每年補貼1500元某市預計2008年職業中專在校生人數是2007年的1.2倍,于是要在2007年的基礎上增加補貼600萬元。2008年該市職業中專在校生有多少萬人?補貼多少萬元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】據電力部門統計,每天8:00至21:00是用電高峰期,簡稱“峰時”.21:00至次日8:00是用電低谷期,簡稱“谷時”為了緩解供電需求的矛盾,某市電力部門擬逐步統一換裝“峰谷分時”電表,對用電實行“峰谷分時電價”新政策,具體見下表:

小明家對換表后最初使用的95千瓦·時電進行測算,發現比在換表前使用95千瓦·時電節約了5.9元,小明家使用“峰時”電和“谷時”電分別是多少千瓦·時?
查看答案和解析>>
科目:初中數學 來源: 題型:
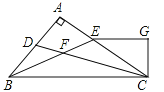
【題目】如圖,△ABC的角平分線 CD、BE相交于F,∠A=90°,EG∥BC,且CG⊥EG于G,下列結論:①∠CEG=2∠DCB;②CA平分∠BCG;③∠ADC=∠GCD;④∠DFB=![]() ∠CGE.
∠CGE.
其中正確的結論是_____________(填序號).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)在如圖所示的數軸上,把數﹣2, ![]() ,4,﹣
,4,﹣![]() ,2.5表示出來,并用“<“將它們連接起來;
,2.5表示出來,并用“<“將它們連接起來;
(2)假如在原點處放立一擋板(厚度不計),有甲、乙兩個小球(忽略球的大小,可看作一點),小球甲從表示數﹣2的點處出發,以1個單位長度/秒的速度沿數軸向左運動;同時小球乙從表示數4的點處出發,以2個單位長度/秒的速度沿數軸向左運動,在碰到擋板后即刻按原來的速度向相反的方向運動,設運動的時間為t(秒).
請從A,B兩題中任選一題作答.
A.當t=3時,求甲、乙兩小球之間的距離.
B.用含t的代數式表示甲、乙兩小球之間的距離.
![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,BE,CD分別為其角平分線且交于點O.
(1)當∠A=60°時,求∠BOC的度數;
(2)當∠A=100°時,求∠BOC的度數;
(3)當∠A=α時,求∠BOC的度數.

查看答案和解析>>
科目:初中數學 來源: 題型:
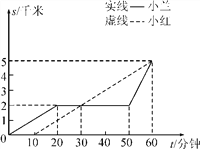
【題目】小紅與小蘭從學校出發到距學校5千米的書店買書,如圖反應了他們兩人離開學校的路程與時間的關系.請根據圖形解決問題.
(1)小紅與小蘭誰先出發?早出發幾分鐘?
(2)小蘭前20分鐘的速度和最后10分鐘的速度各是多少?
(3)小紅與小蘭從學校到書店的平均速度各是多少?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com