
【題目】如圖,Rt△ABC,∠ACB=90°,AC=3,BC=4,將邊AC沿CE翻折,使點A落在AB上的點D處;再將邊BC沿CF翻折,使點B落在CD的延長線上的點B′處,兩條折痕與斜邊AB分別交于點E、F,則線段B′F的長為 . 
【答案】![]()
【解析】解:根據折疊的性質可知CD=AC=3,B′C=BC=4,∠ACE=∠DCE,∠BCF=∠B′CF,CE⊥AB, ∴B′D=4﹣3=1,∠DCE+∠B′CF=∠ACE+∠BCF,
∵∠ACB=90°,
∴∠ECF=45°,
∴△ECF是等腰直角三角形,
∴EF=CE,∠EFC=45°,
∴∠BFC=∠B′FC=135°,
∴∠B′FD=90°,
∵S△ABC= ![]() ACBC=
ACBC= ![]() ABCE,
ABCE,
∴ACBC=ABCE,
∵根據勾股定理求得AB=5,
∴CE= ![]() ,
,
∴EF= ![]() ,ED=AE=
,ED=AE= ![]() ,
,
∴DF=EF﹣ED= ![]() ,
,
∴B′F= ![]() .
.
故答案為: ![]() .
.
首先根據折疊可得CD=AC=3,B′C=BC=4,∠ACE=∠DCE,∠BCF=∠B′CF,CE⊥AB,然后求得△ECF是等腰直角三角形,進而求得∠B′FD=90°,CE=EF= ![]() ,ED=AE=
,ED=AE= ![]() ,從而求得B′D=1,DF=
,從而求得B′D=1,DF= ![]() ,在Rt△B′DF中,由勾股定理即可求得B′F的長.
,在Rt△B′DF中,由勾股定理即可求得B′F的長.


 輕松暑假總復習系列答案
輕松暑假總復習系列答案科目:初中數學 來源: 題型:
【題目】學校決定購買A、B兩種型號電腦,若購買A型電腦3臺,B型電腦8臺共需40000元;若購買A型電腦14臺,B型電腦4臺共需80000元.
(1)A、B兩種型號電腦每臺多少元?
(2)若用不超過160000元去購買A、B兩種型號電腦共45臺,則最多可購買A型電腦多少臺?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲乙二人在400米的環形跑道上練習同向競走.乙每分鐘走80米,甲每分鐘走100米,現在甲在乙前100米,多少分鐘后兩人相遇?( )
A.5分鐘
B.20分鐘
C.15分鐘
D.10分鐘
查看答案和解析>>
科目:初中數學 來源: 題型:
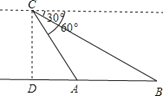
【題目】某日,正在我國南海海域作業的一艘大型漁船突然發生險情,相關部門接到求救信號后,立即調遣一架直升飛機和一艘剛在南海巡航的漁政船前往救援.當飛機到達距離海面3000米的高空C處,測得A處漁政船的俯角為60°,測得B處發生險情漁船的俯角為30°,請問:此時漁政船和漁船相距多遠?(結果保留根號)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在五邊形ABCDE中,∠BAE=120°,∠B=∠E=90°,AB=BC=1,AE=DE=2,在BC,DE上分別找一點M,N,使△AMN的周長最小,則△AMN的最小周長為 . 
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com