
【題目】某景區內的環形路是邊長為800米的正方形ABCD,如圖1和圖2.現有1號、2號兩游覽車分別從出口A和景點C同時出發,1號車順時針、2號車逆時針沿環形路連續循環行駛,供游客隨時免費乘車(上、下車的時間忽略不計),兩車速度均為200米/分. 
探究:設行駛吋間為t分.
(1)當0≤t≤8時,分別寫出1號車、2號車在左半環線離出口A的路程y1 , y2(米)與t(分)的函數關系式,并求出當兩車相距的路程是400米時t的值;
(2)t為何值時,1號車第三次恰好經過景點C?并直接寫出這一段時間內它與2號車相遇過的次數.
(3)發現:如圖2,游客甲在BC上的一點K(不與點B,C重合)處候車,準備乘車到出口A,設CK=x米. 情況一:若他剛好錯過2號車,便搭乘即將到來的1號車;
情況二:若他剛好錯過1號車,便搭乘即將到來的2號車.
比較哪種情況用時較多?(含候車時間)
決策:己知游客乙在DA上從D向出口A走去.步行的速度是50米/分.當行進到DA上一點P (不與點D,A重合)時,剛好與2號車迎面相遇.
他發現,乘1號車會比乘2號車到出口A用時少,請你簡要說明理由:
(4)設PA=s(0<s<800)米.若他想盡快到達出口A,根據s的大小,在等候乘1號車還是步行這兩種方式中.他該如何選擇?
【答案】
(1)解:由題意,得y1=200t,y2=﹣200t+1600
當相遇前相距400米時,﹣200t+1600﹣200t=400,t=3,
當相遇后相距400米時,200t﹣(﹣200t+1600)=400,t=5.
答:當兩車相距的路程是400米時t的值為3分鐘或5分鐘
(2)解:由題意得:1號車第三次恰好經過景點C行駛的路程為:800×2+800×4×2=8000,
∴1號車第三次經過景點C需要的時間為:8000÷200=40分鐘,
兩車第一次相遇的時間為:1600÷400=4.
第一次相遇后兩車每相遇一次需要的時間為:800×4÷400=8,
∴兩車相遇的次數為:(40﹣4)÷8+1=5次.
∴這一段時間內它與2號車相遇的次數為:5次;
發現:由題意,得
情況一需要時間為: ![]() =16﹣
=16﹣ ![]() ,
,
情況二需要的時間為: ![]() =16+
=16+ ![]()
∵16﹣ ![]() <16+
<16+ ![]()
∴情況二用時較多.
(3)解:∵游客乙在AD邊上與2號車相遇,
∴此時1號車在CD邊上,
∴乘1號車到達A的路程小于2個邊長,乘2號車的路程大于3個邊長,
∴乘1號車的用時比2號車少.
(4)解:若步行比乘1號車的用時少,
![]() ,
,
∴s<320.
∴當0<s<320時,選擇步行.
同理可得
當320<s<800時,選擇乘1號車,
當s=320時,選擇步行或乘1號車一樣.
【解析】探究:(1)由路程=速度×時間就可以得出y1 , y2(米) 與t(分)的函數關系式,再由關系式就可以求出兩車相距的路程是400米時t的值;(2)求出1號車3次經過A的路程,進一步求出行駛的時間,由兩車第一次相遇后每相遇一次需要的時間就可以求出相遇次數; 發現:分別計算出情況一的用時和情況二的用時,在進行大小比較就可以求出結論決策:(3)根據題意可以得出游客乙在AD上等待乘1號車的距離小于邊長,而成2號車到A出口的距離大于3個邊長,進而得出結論;(4)分類討論,若步行比乘1號車的用時少,就有 ![]() ,得出s<320.就可以分情況得出結論.
,得出s<320.就可以分情況得出結論.
【考點精析】本題主要考查了一元一次不等式組的應用的相關知識點,需要掌握1、審:分析題意,找出不等關系;2、設:設未知數;3、列:列出不等式組;4、解:解不等式組;5、檢驗:從不等式組的解集中找出符合題意的答案;6、答:寫出問題答案才能正確解答此題.


科目:初中數學 來源: 題型:
【題目】2017年5月31日,昌平區舉辦了首屆初二年級學生“數學古文化閱讀展示”活動,為表彰在本次活動中表現優秀的學生,老師決定在6月1日購買筆袋或彩色鉛筆作為獎品. 已知1個筆袋、2筒彩色鉛筆原價共需44元;2個筆袋、3筒彩色鉛筆原價共需73元.
(1)每個筆袋、每筒彩色鉛筆原價各多少元?
(2)時逢“兒童節”,商店舉行“優惠促銷”活動,具體辦法如下:筆袋“九折”優惠;彩色鉛筆不超過10筒不優惠,超出10筒的部分“八折”優惠. 若買x個筆袋需要y1元,買x筒彩色鉛筆需要y2元. 請用含x的代數式表示y1、y2;
(3)若在(2)的條件下購買同一種獎品95件,請你分析買哪種獎品省錢.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:如下圖, AB∥CD , 點E , F分別為AB , CD上一點.
(1)在AB , CD之間有一點M(點M不在線段EF上),連接ME , MF , 試探究∠AEM , ∠EMF , ∠MFC之間有怎樣的數量關系. 請補全圖形,并在圖形下面寫出相應的數量關系,選其中一個進行證明.
(2)如下圖,在AB , CD之間有兩點M , N , 連接ME , MN , NF , 請選擇一個圖形寫出∠AEM , ∠EMN , ∠MNF , ∠NFC 存在的數量關系(不需證明).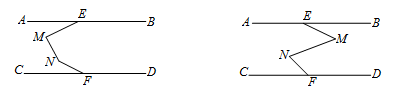
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,某工程隊從A點出發,沿北偏西67度方向修一條公路AD,在BD路段出現塌陷區,就改變方向,由B點沿北偏東23度的方向繼續修建BC段,到達C點又改變方向,使所修路段CE∥AB,此時∠ECB有多少度?試說明理由.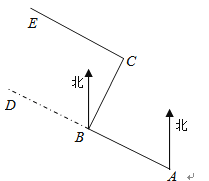
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com