【題目】關于x的一元二次方程ax2﹣3x﹣1=0的兩個不相等的實數根都在﹣1和0之間（不包括﹣1和0），則a的取值范圍是 ．
【答案】
＜a＜﹣2
【解析】解：∵關于x的一元二次方程ax2﹣3x﹣1=0的兩個不相等的實數根
∴△=（﹣3）2﹣4×a×（﹣1）＞0，
解得：a＞ 
設f（x）=ax2﹣3x﹣1，如圖，
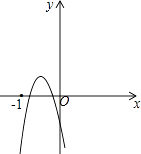
∵實數根都在﹣1和0之間，
∴﹣1 
，
∴a 
，
且有f（﹣1）＜0，f（0）＜0，
即f（﹣1）=a×（﹣1）2﹣3×（﹣1）﹣1＜0，f（0）=﹣1＜0，
解得：a＜﹣2，
∴ ＜a＜﹣2，
所以答案是： ＜a＜﹣2．
【考點精析】掌握拋物線與坐標軸的交點是解答本題的根本，需要知道一元二次方程的解是其對應的二次函數的圖像與x軸的交點坐標．因此一元二次方程中的b2-4ac，在二次函數中表示圖像與x軸是否有交點．當b2-4ac>0時，圖像與x軸有兩個交點；當b2-4ac=0時，圖像與x軸有一個交點；當b2-4ac<0時，圖像與x軸沒有交點．
天天向上一本好卷系列答案
小學生10分鐘應用題系列答案科目：初中數學 來源： 題型：
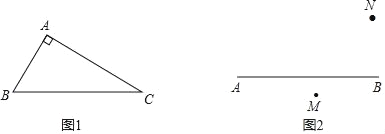
【題目】(1)如圖1，在Rt△ABC中，AB＝3，AC＝4，BC＝5，若直線EF垂直平分BC，請你利用尺規畫出直線EF；
(2)若點P在(1)中BC的垂直平分線EF上，請直接寫出PA+PB的最小值，回答PA+PB取最小值時點P的位置并在圖中標出來；
解：PA+PB的最小值為 ，PA+PB取最小值時點P的位置是 ；
(3)如圖2，點M，N分別在直線AB兩側，在直線AB上找一點Q，使得∠MQB＝∠NQB．要求畫圖，并簡要敘述確定點Q位置的步驟(無需尺規作圖，保留畫圖痕跡，無需證明)
解：確定點Q位置的簡要步驟： ．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在《科學》課上，老師講到溫度計的使用方法及液體的沸點時，好奇的王紅同學準備測量食用油的沸點，已知食用油的沸點溫度高于水的沸點溫度（
），王紅家只有刻度不超過的溫度計，她的方法是在鍋中倒入一些食用油，用煤氣灶均勻加熱，并每隔
測量一次鍋中油溫，測量得到的數據如下表：
時間 | 0 | 10 | 20 | 30 | 40 |
油溫 | 10 | 30 | 50 | 70 | 90 |
王紅發現，燒了
時，油沸騰了，則下列說法不正確的是（ ）
A. 沒有加熱時，油的溫度是
B. 加熱
，油的溫度是
C. 估計這種食用油的沸點溫度約是
D. 每加熱，油的溫度升高
查看答案和解析>>
科目：初中數學 來源： 題型：
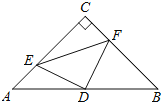
【題目】如圖，在
中，
，
，D是AB的中點，點E、F分別在AC、BC邊上運動
點E不與點A、C重合
，且保持
，連接DE、DF、
在此運動變化的過程中，有下列結論：
；
四邊形CEDF的面積隨點E、F位置的改變而發生變化；
；
以上結論正確的是______只填序號．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某學習小組在探究三角形全等時，發現了下面這種典型的基本圖形：
如圖1，已知：在
中，
，
，直線m經過點A，
直線m，
直線m，垂足分別為點D、
試猜想DE、BD、CE有怎樣的數量關系，請直接寫出；
組員小穎想，如果三個角不是直角，那結論是否會成立呢？如圖2，將中的條件改為：在中，，D、A、E三點都在直線m上，并且有
其中
為任意銳角或鈍角
如果成立，請你給出證明；若不成立，請說明理由．
數學老師贊賞了他們的探索精神，并鼓勵他們運用這個知識來解決問題：
如圖3，F是
角平分線上的一點，且
和
均為等邊三角形，D、E分別是直線m上A點左右兩側的動點
、E、A互不重合
，在運動過程中線段DE的長度始終為n，連接BD、CE，若
，試判斷
的形狀，并說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】綜合題：探索發現
（1）自主閱讀：在三角形的學習過程，我們知道三角形一邊上的中線將三角形分成了兩個面積相等三角形，原因是兩個三角形的底邊和底邊上的高都相等，在此基礎上我們可以繼續研究：如圖1，AD∥BC，連接AB，AC，BD，CD，則S△ABC=S△BCD ．
證明：分別過點A和D，作AF⊥BC于F．DE⊥BC于E，由AD∥BC，可得AF=DE，又因為S△ABC= 
×BC×AF，S△BCD= 
．
所以S△ABC=S△BCD
由此我們可以得到以下的結論：像圖1這樣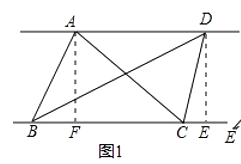
（2）問題解決：如圖2，四邊形ABCD中，AB∥DC，連接AC，過點B作BE∥AC，交DC延長線于點E，連接點A和DE的中點P，請你運用上面的結論證明：SABCD=S△APD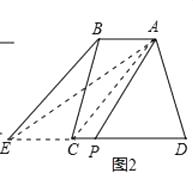
（3）應用拓展：
如圖3，按此方式將大小不同的兩個正方形放在一起，連接AF，CF，若大正方形的面積是80cm2 ， 則圖中陰影三角形的面積是cm2 ．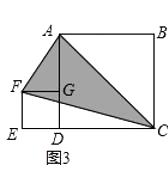 
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】為更新果樹品種，某果園計劃新購進A、B兩個品種的果樹苗栽植培育，若計劃購進這兩種果樹苗共45棵，其中A種樹苗的單價為7元/棵，購買B種苗所需費用y（元）與購買數量x（棵）之間存在如圖所示的函數關系．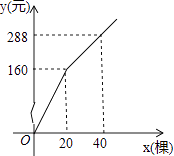
（1）求y與x的函數關系式；
（2）若在購買計劃中，B種樹苗的數量不超過35棵，但不少于A種樹苗的數量，請設計購買方案，使總費用最低，并求出最低費用．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，每個小正方形的邊長為1，在方格紙內將△ABC經過一次平移后得到△A′B′C′，圖中標出了點B的對應點B′．根據下列條件，利用網格點和直尺畫圖：
（1）補全△A′B′C′；
（2）作出△ABC的中線CD；
（3）畫出BC邊上的高線AE；
（4）若△ABC與△ABE面積相等，則圖中滿足條件且異于點C的格點E共有 個．（注：格點指網格線的交點）
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
