
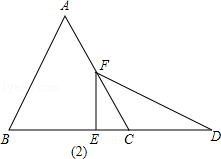
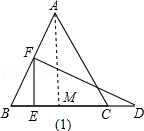
 ,現將△DEF沿直線BC以每秒
,現將△DEF沿直線BC以每秒 個單位向右平移,直至E點與C點重合時停止運動,設運動時間為t秒.
個單位向右平移,直至E點與C點重合時停止運動,設運動時間為t秒. ?若存在,試求出CH的值;若不存在,請說明理由.
?若存在,試求出CH的值;若不存在,請說明理由.
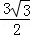 (12﹣t)2 (3)見解析
(12﹣t)2 (3)見解析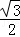 AB=
AB=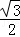 ×6
×6 =9,
=9,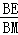 =
=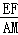 ,即
,即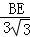 =
=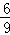 ,解得:BE=2
,解得:BE=2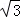 ,則移動的距離是:6
,則移動的距離是:6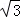 +2
+2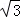 =8
=8 ,則t=
,則t=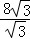 =8;
=8; ,則移動的距離是:2×6
,則移動的距離是:2×6 ﹣2
﹣2 =12
=12 ﹣2
﹣2 =10
=10 ,則t=
,則t= =10,
=10,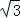 t,
t,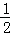 BD=
BD=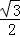 t,ND=
t,ND=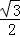 BD=
BD= ×
× t=
t=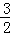 t,則s=
t,則s= NB•ND=
NB•ND= ×
× t×
t×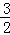 t=
t= t2;
t2; t﹣6
t﹣6 ,
, t﹣6
t﹣6 ,
, TC=
TC=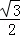 (
( t﹣6
t﹣6 )=
)= t﹣9,
t﹣9,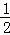 CD•TH=18﹣
CD•TH=18﹣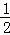 (
( t﹣6
t﹣6 )(
)(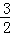 t﹣9)=﹣
t﹣9)=﹣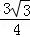 (t﹣6)2+18;
(t﹣6)2+18; ﹣
﹣ t,
t, EC=
EC=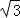 (12
(12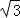 ﹣
﹣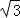 t),
t),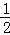 EC•EJ=
EC•EJ=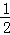 ×
×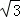 (12
(12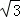 ﹣
﹣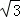 t)2=
t)2=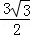 (12﹣t)2.
(12﹣t)2.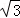 ×
× =6,
=6,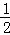 x,
x, x2,
x2,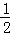 BC•HL=3
BC•HL=3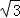 ×
×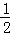 x=
x= x,
x,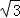 x.
x. x﹣
x﹣ x﹣
x﹣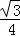 x2=4
x2=4 ,方程無解.
,方程無解. x2+
x2+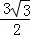 x﹣3
x﹣3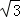 x=4
x=4 ,解得:x=8或﹣2(舍去),故x=8
,解得:x=8或﹣2(舍去),故x=8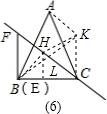




 優(yōu)生樂園系列答案
優(yōu)生樂園系列答案 新編小學單元自測題系列答案
新編小學單元自測題系列答案科目:初中數學 來源:不詳 題型:解答題
查看答案和解析>>
科目:初中數學 來源:不詳 題型:解答題
查看答案和解析>>
科目:初中數學 來源:不詳 題型:填空題
查看答案和解析>>
科目:初中數學 來源:不詳 題型:解答題
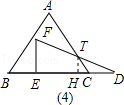
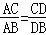 ,
, 是否都成立?
是否都成立?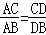 一定成立嗎?并證明你的判斷.
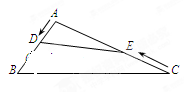
一定成立嗎?并證明你的判斷.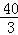 ,E為AB上一點且AE=5,CE交其內角角平分線AD于F.試求
,E為AB上一點且AE=5,CE交其內角角平分線AD于F.試求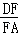 的值.
的值.
查看答案和解析>>
科目:初中數學 來源:不詳 題型:解答題
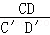 等于多少?
等于多少?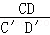 等于多少?如果CD和C′D′是它們的對應中線呢?
等于多少?如果CD和C′D′是它們的對應中線呢?查看答案和解析>>
科目:初中數學 來源:不詳 題型:填空題
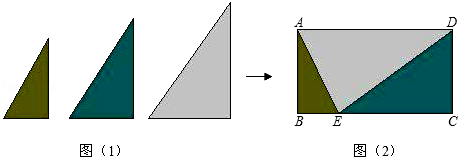
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com