
【題目】如圖,已知AB是⊙O的直徑,P為⊙O外一點,且OP∥BC,∠P=∠BAC. 
(1)求證:PA為⊙O的切線;
(2)若OB=5,OP= ![]() ,求AC的長.
,求AC的長.
【答案】
(1)證明:∵AB是⊙O的直徑,
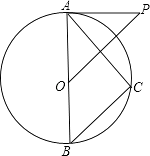
∴∠ACB=90°,
∴∠BAC+∠B=90°.
又∵OP∥BC,
∴∠AOP=∠B,
∴∠BAC+∠AOP=90°.
∵∠P=∠BAC.
∴∠P+∠AOP=90°,
∴由三角形內角和定理知∠PAO=90°,即OA⊥AP.
又∵OA是的⊙O的半徑,
∴PA為⊙O的切線
(2)解:由(1)知,∠PAO=90°.∵OB=5,
∴OA=OB=5.
又∵OP= ![]() ,
,
∴在直角△APO中,根據勾股定理知PA= ![]() =
= ![]() ,
,
由(1)知,∠ACB=∠PAO=90°.
∵∠BAC=∠P,
∴△ABC∽△POA,
∴ ![]() =
= ![]() .
.
∴ ![]() =
= ![]() ,
,
解得AC=8.即AC的長度為8.
【解析】(1)欲證明PA為⊙O的切線,只需證明OA⊥AP;(2)通過相似三角形△ABC∽△PAO的對應邊成比例來求線段AC的長度.
【考點精析】本題主要考查了勾股定理的概念和切線的判定定理的相關知識點,需要掌握直角三角形兩直角邊a、b的平方和等于斜邊c的平方,即;a2+b2=c2;切線的判定方法:經過半徑外端并且垂直于這條半徑的直線是圓的切線才能正確解答此題.


科目:初中數學 來源: 題型:
【題目】如圖所示,Rt△ABC中,∠BAC=90°,∠C=30°,BC=2,⊙O是△ABC的外接圓,D是CB延長線上一點,且BD=1,連接DA,點P是射線DA上的動點. 
(1)求證DA是⊙O的切線;
(2)DP的長度為多少時,∠BPC的度數最大,最大度數是多少?請說明理由.
(3)P運動的過程中,(PB+PC)的值能否達到最小,若能,求出這個最小值,若不能,說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀下列材料:
社會消費品零售總額是指批發和零售業,住宿和餐飲業以及其他行業直接售給城鄉居民和社會集團的消費品零售額,在各類與消費有關的統計數據中,社會消費品零售總額是表現國內消費需求最直接的數據.
2012年,北京市全年實現社會消費品零售總額7702.8億元,比上一年增長11.6%,2013年,全年實現社會消費品零售總額8375.1億元,比上一年增長8.7%,2014年,全年實現社會消費品零售總額9098.1億元,比上一年增長8.6%,2015年,全年實現社會消費品零售總額10338億元,比上一年增長7.3%.
2016年,北京市實現市場總消費19926.2億元,比上一年增長了8.1%,其中實現服務性消費8921.1億元,增長10.1%;實現社會消費品零售總額11005.1億元,比上一年增長了6.5%.
根據以上材料解答下列問題:
(1)補全統計表:
2012﹣2016年北京市社會消費品零售總額統計表
年份 | 2012年 | 2013年 | 2014年 | 2015年 | 2016年 |
社會消費品零售總額(單位:億元) |
(2)選擇適當的統計圖將2012﹣2016年北京市社會消費品零售總額比上一年的增長率表示出來,并在圖中表明相應數據;
(3)根據以上信息,估計2017年北京市社會消費品零售總額比上一年的增長率約為 , 你的預估理由是 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在正方形ABCD中,點E在AB邊上,點F在BC邊的延長線上,且AE=CF 
(1)求證:△AED≌△CFD;
(2)將△AED按逆時針方向至少旋轉多少度才能與△CFD重合,旋轉中心是什么?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,所有正三角形的一邊平行于x軸,一頂點在y軸上.從內到外,它們的邊長依次為2,4,6,8,…,頂點依次用A1、A2、A3、A4…表示,其中A1A2與x軸、底邊A1A2與A4A5、A4A5與A7A8、…均相距一個單位,則頂點A3的坐標是 , A92的坐標是 . 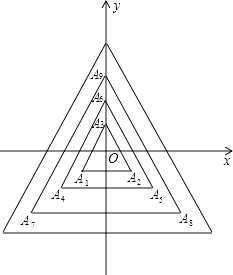
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,我國漁政船在釣魚島海域C處測得釣魚島A在漁政船的北偏西30°的方向上,隨后漁政船以80海里/小時的速度向北偏東30°的方向航行,半小時后到達B處,此時又測得釣魚島A在漁政船的北偏西60°的方向上,求此時漁政船距釣魚島A的距離AB.(結果保留小數點后一位,其中 ![]() =1.732)
=1.732)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】若x1 , x2(x1<x2)是方程(x﹣a)(x﹣b)=1(a<b)的兩個根,則實數x1 , x2 , a,b的大小關系為( )
A.x1<x2<a<b
B.x1<a<x2<b
C.x1<a<b<x2
D.a<x1<b<x2
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某公司生產的某種商品每件成本為20元,經過市場調研發現,這種商品在未來40天內的日銷售量m(件)與時間t(天)的關系如下表:
時間t(天) | 1 | 3 | 5 | 10 | 36 | … |
日銷售量m(件) | 94 | 90 | 86 | 76 | 24 | … |
未來40天內,前20天每天的價格y1(元/件)與時間t(天)的函數關系式為y1= ![]() t+25(1≤t≤20且t為整數),后20天每天的價格y2(元/件)與時間t(天)的函數關系式為y2=﹣
t+25(1≤t≤20且t為整數),后20天每天的價格y2(元/件)與時間t(天)的函數關系式為y2=﹣ ![]() t+40(21≤t≤40且t為整數).
t+40(21≤t≤40且t為整數).
下面我們就來研究銷售這種商品的有關問題:
(1)認真分析上表中的數據,用所學過的一次函數、二次函數、反比例函數的知識確定一個滿足這些數據的m(件)與t(天)之間的表達式;
(2)請預測未來40天中哪一天的日銷售利潤最大,最大日銷售利潤是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲、乙兩條輪船同時從港口A出發,甲輪船以每小時30海里的速度沿著北偏東60°的方向航行,乙輪船以每小時15海里的速度沿著正東方向行進,1小時后,甲船接到命令要與乙船會合,于是甲船改變了行進的速度,沿著東南方向航行,結果在小島C處與乙船相遇.假設乙船的速度和航向保持不變,求:
(1)港口A與小島C之間的距離;
(2)甲輪船后來的速度.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com