【題目】如圖，M是△ABC的邊BC的中點，AN平分
，BN
AN于點N，延長BN交AC于點D，已知AB=10，AC=16.
（1）求證：BN=DN；
（2）求MN的長.
科目：初中數學 來源： 題型：
【題目】問題發現：數學興趣小組在活動時，老師提出了這樣一個問題：如圖①，在Rt△ABC中，∠BAC＝90°，BC＝10，AD是BC邊上的中線，求AD的長度．小明在組內經過合作交流，得到了如下的解決方法：延長AD到E，使DE＝AD，則AD＝
AE
在△ADC和△EDB中
∴△ADC≌△EDB
∴∠DBE＝∠DCA，BE＝AC
∴BE∥AC
∴∠EBA+∠BAC＝180°
∵∠BAC＝90°
∴∠EBA＝90°
在△EBA和△CAB中
∴△EBA≌△CAB
∴AE＝BC
∵BC＝10
∴AD＝AE＝BC＝5
（1）若將上述問題中條件“BC＝10”換成“BC＝a”，其他條件不變，則可得AD＝ ．
從上得到結論：直角三角形斜邊上的中線，等于斜邊的一半．
（感悟）解題時，條件中若出現“中點”“中線”等字樣，可以考慮延長中線構造全等三角形進而求解．
問題解決：（2）如圖②，在四邊形ABCD中，AD∥BC，∠D＝90°，M是AB的中點．若CM＝6.5，BC+CD+DA＝17，求四邊形ABCD的面積．
問題拓展：（3）如圖③，在平行四邊形ABCD中，AD＝2AB，F是AD的中點，作CE⊥AB，垂足E在線段AB上，連接EF、CF，∠DFE與∠AEF的度數滿足數量關系：∠DFE＝k∠AEF，求k的值．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】小明家住房戶型呈長方形，平面圖如下（單位：米）．現準備鋪設整個長方形地面，其中三間臥室鋪設木地板，其它區域鋪設地磚．（房間內隔墻寬度忽略不計）
（1）求a的值；
（2）請用含x的代數式分別表示鋪設地面需要木地板和地磚各多少平方米；
（3）按市場價格，木地板單價為300元/平方米，地磚單價為100元/平方米．裝修公司有A，B兩種活動方案，如表：
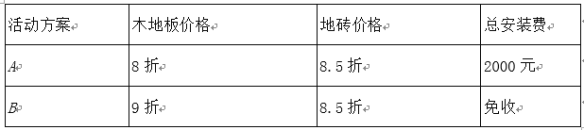
已知臥室2的面積為21平方米，則小方家應選擇哪種活動，使鋪設地面總費用（含材料費及安裝費）更低？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某物流公司現有114噸貨物，計劃同時租出A，B兩種型號的車，王經理發現一個運貨貨單上的一個信息是：
A型車（滿載） | B型車（滿載） | 運貨總量 |
3輛 | 2輛 | 38噸 |
1輛 | 3輛 | 36噸 |
根據以上信息，解析下列問題：
（1）1輛A型車和1輛B型車都裝滿貨物一次可分別運貨多少噸？
（2）若物流公司打算一次運完，且恰好每輛車都裝滿貨物，請你幫該物流公司設計租車方案。
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在平面直角坐標系中，矩形
的頂點
、
的坐標分別為
，
，點
是
的中點，點
在
上運動，點
是坐標平面內的任意一點．若以
、、、為頂點的四邊形是邊長為5的菱形時，則點的坐標為__________．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，矩形
中，
，
，
、
分別是
、
上的點，且
，連結
、
．點
是線段
上的點，過點作
交
于點
，設AP=x．
（1）求證：四邊形
是菱形；
（2）用含
的代數式表示
的長；
（3）連結
，當為何值時
．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】下圖是南通市1995-2001年國內生產總值增長率變化情況，下列結論不正確的是（ ）
A.1995-1998年，南通市國內生產總值的年增長率逐年減小
B.自1998年以來，南通市國內生產總值的年增長率開始回升
C.1995年-2001年，南通市每年的國內生產總值有增有減
D.1995年-2001年，南通市每年的國內生產總值不斷增長
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
