【題目】如圖，在△ABC 中，∠C=90°
（1）利用尺規作∠B 的角平分線交AC于D，以BD為直徑作⊙O交AB于E（保留作圖痕跡，不寫作法）；
（2）綜合應用：在（1）的條件下，連接DE
①求證：CD=DE；
②若sinA=
，AC=6，求AD．
【答案】（1）作圖見解析；（2）①證明見解析；②AD=
.
【解析】試題分析：（1）利用角平分線的作法得出∠B的角平分線BD，根據線段垂直平分線的作法作出線段BD的垂直平分線，交BD于點O，以O為圓心，以OB長為半徑作圓即可；（2）根據直徑所對的圓周角為直角可得∠BED=90°，再由角平分線的性質可得CD=DE；在Rt△ADE中，sinA=
=
，設DC=DE=3x，AD=5x，根據AC=AD+DC列出方程求得x的值，即可求得AD的長.
試題解析：
（1）
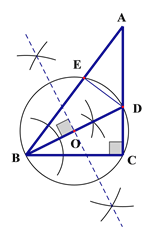
（2）∵BD為
O的直徑
∴∠BED=90°，又∵∠C=90°
∴DE⊥AB，DC⊥BC
又∵BD平分∠ABC
∴DE=DC
（3）
在Rt△ADE中，sinA=
∵sinA=
∴
=
設DC=DE=3
，AD=5
∵AC=AD+DC
∴3
+5
=6
=
AD=5
=5×
=
科目：初中數學 來源： 題型：
【題目】如圖，將矩形紙片ABCD沿對角線BD折疊，使點A落在平面上的F點處，DF交BC于點E．
（1）求證：△DCE≌△BFE；
（2）若CD=6，DB=10，求BE的長．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，已知一次函數y1=（m﹣2）x+2與正比例函數y2=2x圖象相交于點A（2，n），一次函數y1=（m﹣2）x+2與x軸交于點B．
（1）求m、n的值；
（2）求△ABO的面積；
（3）觀察圖象，直接寫出當x滿足 時，y1＞y2．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知二次函數
和一次函數
．
（1）當t=0時，試判斷二次函數
的圖象與x軸是否有公共點，如果有，請寫出公共點的坐標；
（2）若二次函數
的圖象與x軸的兩個不同公共點，且這兩個公共點間的距離為8，求t的值；
（3）求證：不論實數t取何值，總存在實數x，使
≥
．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某商場銷售一批名牌襯衫，平均每天可售出20件，每件盈利44元，為了擴大銷售，增加盈利，盡快減少庫存，商場決定采取適當的降價措施，經調查發現，如果每件襯衫每降價1元，商場平均每天可多售出5件。若商場平均每天要盈利1600元，每件襯衫應降價多少元？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】尺規作圖作∠AOB的平分線方法如下：以O為圓心，任意長為半徑畫弧交OA，OB于C，D，再分別以點C，D為圓心，以大于
CD長為半徑畫弧，兩弧交于點P，作射線OP．由作法得△OCP≌△ODP的根據是（ ）
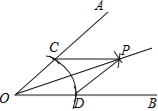
A. SAS B. ASA C. AAS D. SSS
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com