
【題目】如圖,填空:
(1)若∠4=∠3,則____∥_____,理由是______;
(2)若∠2=∠E,則____∥___,理由是____;
(3)若∠A=∠ABE=180°,則____∥___,理由是____;
(4)若∠2=∠____,則DA∥EB,理由是____;
(5)若∠DBC+∠_____=180°,則DB∥EC,理由是____;

【答案】AD, BE, 同位角相等,兩直線平行, BD, CE, 內錯角相等,兩直線平行, AD, BE, 同旁內角互補,兩直線平行, D, 內錯角相等,兩直線平行, C, 同旁內角互補,兩直線平行
【解析】
根據平行線的判定方法解答即可.
(1)若∠4=∠3,則_AD__∥__BE__,理由是;(同位角相等,兩直線平行);
(2)若∠2=∠E,則__BD__∥_CE__,理由是(內錯角相等,兩直線平行);
(3)若∠A=∠ABE=180°,則_AD___∥__BE_,理由是(同旁內角互補,兩直線平行);
(4)若∠2=∠_D___,則DA∥EB,理由是(內錯角相等,兩直線平行);
(5)若∠DBC+∠_C_=180°,則DB∥EC,理由是(同旁內角互補,兩直線平行);
故答案為:(1). AD (2). BE (3). 同位角相等,兩直線平行; (4). BD, (5)CE, (6)內錯角相等,兩直線平行; (7). AD, (8)BE, (9)同旁內角互補,兩直線平行; (10). D (11). 內錯角相等,兩直線平行; (12).C, (13) 同旁內角互補,兩直線平行.


 天天向上口算本系列答案
天天向上口算本系列答案科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,直線AB分別交x、y軸于點A、B,直線BC分別交x、y軸于點C、B,點A的坐標為(3,0),∠ABO=30°,且AB⊥BC.
(1)求直線BC和AB的解析式;
(2)將點B沿某條直線折疊到點O,折痕分別交BC、BA于點E、D,在x軸上是否存在點F,使得點D、E、F為頂點的三角形是以DE為斜邊的直角三角形?若存在,請求出F點坐標;若不存在,請說明理由;
(3)在平面直角坐標系內是否存在兩個點,使得這兩個點與B、C兩點構成的四邊形是正方形?若存在,請求出這兩點的坐標;若不存在,請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,將△ABC沿BC邊上的中線AD平移到△A'B'C'的位置,已知△ABC的面積為9,陰影部分三角形的面積為4.若AA'=1,則A'D等于( )

A. 2 B. 3 C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在下列選項中,是反比例函數關系的為
A. 在直角三角形中,30°角所對的直角邊y與斜邊x之間的關系
B. 在等腰三角形中,頂角y與底角x之間的關系
C. 圓的面積S與它的直徑d之間的關系
D. 面積為20的菱形,其中一條對角線y與另一條對角線x之間的關系
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在兩個不透明的口袋中分別裝有三個顏色分別為紅色、白色、綠色的小球,這三個小球除顏色外其他都相同,
(1)在其中一個口袋中一次性隨機摸出兩個球,請寫出在這一過程中的一個必然事件;
(2)若分別從兩個袋中隨機取出一個球,試求出兩個小球顏色相同的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
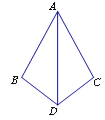
【題目】如圖,在△ADB和△ADC中,下列條件:①BD=DC,AB=AC;②∠B=∠C,∠BAD=∠CAD;③∠B=∠C,BD=DC;④∠ADB=∠ADC,BD=DC.能得出△ADB≌△ADC的序號是 .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com