
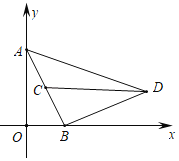
【題目】在平面直角坐標系中,線段AB的兩個端點A(0,2),B(1,0),點C為線段AB的中點.將線段BA繞點B按順時針方向旋轉90°得到線段BD,連結CD,AD.點P是直線BD上的一個動點.
(1)求點D的坐標和直線BD的解析式;
(2)當∠PCD=∠ADC時,求點P的坐標;
(3)若點Q是經過點B,點D的拋物線y=ax2+bx+2上的一個動點,請你探索:是否存在這樣的點Q,使得以點P、點Q、點D為頂點的三角形與△ACD相似.若存在,請求出點P的坐標;若不存在,請說明理由.
【答案】(1)![]() ;(2)點P的坐標為(2,
;(2)點P的坐標為(2,![]() )或(8,
)或(8,![]() );(3)見解析.
);(3)見解析.
【解析】
(1)作DE⊥x軸,構造全等三角形求點D的坐標,待定系數法求BD的解析式;
(2)要特別注意∠PCD=∠ADC有兩種情況:∠PCD在直線CD的下方或上方,防止漏解;
(3)根據∠PDQ分別與∠ACD,∠ADC,∠CAD相等進行討論,每種情形都還要再分兩種情況進行分析,還要注意點在點D的左側和右側兩種不同情況,以防漏解.
解:(1)如圖1,過D作DE⊥x軸于E,由旋轉得:BA=BD,∠ABD=90°,
∵DE⊥x軸,
∴∠BED=∠AOB=90°
∴∠BAO+∠ABO=90°,∠DBE+∠ABO=90°,
∴∠BAO=∠DBE
∴△BAO≌△DBE(AAS)
∴BE=OA=2,DE=OB=1,
∴OE=OB+BE=1+2=3
∴D(3,1);
設直線BD的解析式為y=mx+n,將B(1,0),D(3,1)分別代入得![]() ,解得
,解得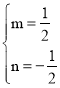 ,
,
∴直線BD的解析式為![]() .
.
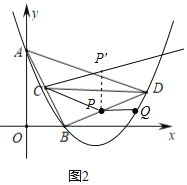
(2)如圖2,∵∠PCD=∠ADC
∴CP∥AD
∴![]() ,
,
∵BC=CA
∴BP=PD
∴P(2,![]() ),
),
作點P關于直線CD的對稱點P′(2,![]() ),連接CP′,則∠P′CD=∠PCD=∠ADC
),連接CP′,則∠P′CD=∠PCD=∠ADC
設直線CP′的解析式為y=m1x+n1,將C(![]() ,1),P′(2,
,1),P′(2,![]() )代入得
)代入得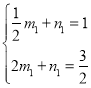 ,解得
,解得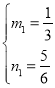 ,
,
∴直線CP′的解析式為![]() ,
,
聯立方程組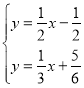 ,解得
,解得![]() ,∴P(8,
,∴P(8,![]() ),
),
綜上所述:點P的坐標為(2,![]() )或(8,
)或(8,![]() ).
).
(3)將B(1,0),D(3,1)分別代入y=ax2+bx+2得![]() ,
,
解得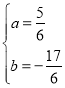 ,
,
∴拋物線解析式為![]() ,
,
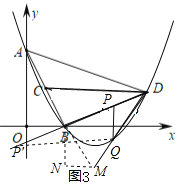
△PDQ與△ACD相似分三種情況:
①如圖3,∠PDQ=∠DAC=45°,延長AB至M,使BM=BD,連接DM交拋物線于Q,
作BN∥y軸,MN∥x軸交BN于N,
∴BM=BD=![]() ,∠MBN=∠BAO,∠BNM=90°
,∠MBN=∠BAO,∠BNM=90°
∴![]() =tan∠MBN=tan∠BAO=
=tan∠MBN=tan∠BAO=![]() ,
,
∴MN=1,BN=2,
∴M(2,﹣2);
設直線DM解析式為y=m2x+n2,將D(3,1)、M(﹣2,﹣2)代入,
得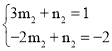 ,
,
解得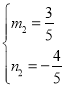
∴直線DM解析式為![]()
聯立方程組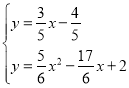 ,
,
解得![]() (舍去),
(舍去),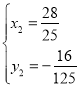
Q![]() ;
;
若∠DPQ=∠ACD,則可證得PQ∥y軸,
∴P1![]() ,
,
若∠DPQ=∠ADC,可求得
P2![]() ,
,
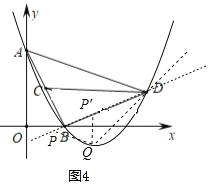
②∠PDQ=∠ADC時,
如圖4,點Q位于直線BD下方時,
∠PDQ+∠CDB=∠ADC+∠CDB,即∠CDQ=∠ADB=45°,
∵CD∥x軸,∴直線DQ與x軸夾角為45°,設DQ解析式為y=x+k,將D(3,1)代入得3+k=1,k=﹣2
∴y=x﹣2
聯立方程組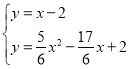 ,
,
解得![]() (舍去),
(舍去),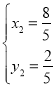 ,
,
∴![]() ,
,
易求直線AD解析式為![]() ,
,
∴直線PQ解析式為![]()
聯立方程組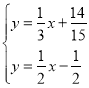 ,解得
,解得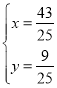 ,
,
∴P3![]() ,
,
若∠DPQ=∠ACD,則PQ∥y軸,![]() ;
;
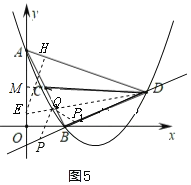
如圖5,點Q位于直線BD上方時,
在y軸上取點E(0,![]() ),延長DC交y軸于點M,連接DE交拋物線于Q,過點E作EH⊥AD于H,
),延長DC交y軸于點M,連接DE交拋物線于Q,過點E作EH⊥AD于H,
作∠DQP1=45°或∠DQP=∠ACD,點P,P1在直線BD上,
在Rt△AEH中,tan∠ADM中,tan∠DAM=![]() =3,AM=1,DM=3,AM=
=3,AM=1,DM=3,AM=![]() ;
;
在Rt△AEH中,tan∠EAD=![]() =3,AE=AO﹣OE=2﹣
=3,AE=AO﹣OE=2﹣![]() ,
,
設AH=x,則EH=3x,
由勾股定理得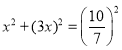 ,解得x=
,解得x=![]() ,
,
∴EH=![]() ,DH=
,DH=![]()
∴tan∠EDA=![]() =tan∠BAC
=tan∠BAC
∴∠EDA=∠BAC
∴∠BDQ=∠ADC
易求得直線DE解析式為y=![]() ,可聯立方程組解得Q
,可聯立方程組解得Q![]() ,
,
若∠DQP=∠DAC=45°,易求得DQ=![]() ,
,
由△ADC∽△QDP得![]() ,
,
∴DP×DA=DC×DQ,即![]() ,
,
∴DP=![]()
∴P5![]() .
.
若∠DPQ=∠DAC=45°,
由△DPQ∽△DAC得![]()
∴DP×DC=DA×DQ,即DP×![]()
∴DP=![]()
∴P6![]()
③如圖6,∠PDQ=∠ACD,
當點P在射線DB上時,
∵∠ACD=∠CDB+∠CBD=∠CDB+90°
∴DQ⊥CD時,∠BDQ=∠ACD,顯然,此時點Q不存在.
當點P在DB反向延長線上時,
易求得直線DQ解析式為y=![]() ,
,
聯立方程組可求得Q![]() ,
,
∴DQ=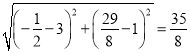
若∠PQD=∠ADC,則△DPQ∽△CAD
∴![]() ,即DP×CD=CA×DQ,DP×
,即DP×CD=CA×DQ,DP×![]()
∴DP=![]()
∴P7![]() ,
,
若∠PQD=∠DAC,則△DPQ∽△CDA
∴![]() ,即DP×CA=CD×DQ,DP×
,即DP×CA=CD×DQ,DP×![]()
∴DP=![]()
∴P8![]()
綜上所述:符合要求的點P的坐標為P1![]() ,P2
,P2![]() ,P3
,P3![]() ,
,![]() ; P5
; P5![]() ,P6
,P6![]() ,P7
,P7![]() ,P8
,P8![]() .
.



科目:初中數學 來源: 題型:
【題目】如圖,AB是半圓O的直徑,點P是半圓上不與點A,B重合的動點,PC∥AB,點M是OP中點.
(1)求證:四邊形OBCP是平行四邊形;
(2)填空:
①當∠BOP= 時,四邊形AOCP是菱形;
②連接BP,當∠ABP= 時,PC是⊙O的切線.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】紅星公司生產的某種時令商品每件成本為20元,經過市場調研發現,這種商品在未來40天內的 日銷售量(件)與時間(天)的關系如下表:
時間(天) | 1 | 3 | 6 | 10 | 36 | … |
日銷售量(件) | 94 | 90 | 84 | 76 | 24 | … |
未來40天內,前20天每天的價格y1(元/件)與t時間(天)的函數關系式為:y1=![]() t+25(1≤t≤20且t為整數);后20天每天的價格y2(原/件)與t時間(天)的函數關系式為:y2=—
t+25(1≤t≤20且t為整數);后20天每天的價格y2(原/件)與t時間(天)的函數關系式為:y2=—![]() t+40(21≤t≤40且t為整數).下面我們來研究 這種商品的有關問題.
t+40(21≤t≤40且t為整數).下面我們來研究 這種商品的有關問題.
(1)認真分析上表中的數量關系,利用學過的一次函數、二次函數 、反比例函數的知識確定一個滿足這些數據之間的函數關系式;
(2)請預測未來40天中那一天的銷售利潤最大,最大日銷售利潤是多少?
(3)在實際銷售的前20天中該公司決定每銷售一件商品就捐贈a元利潤(a<4)給希望工程,公司通過銷售記錄發現,前20天中,每天扣除捐贈后的日銷售利潤隨時間t的增大而增大,求a的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在一條筆直的東西向海岸線l上有一長為1.5km的碼頭MN和燈塔C,燈塔C距碼頭的東端N有20km.一輪船以36km/h的速度航行,上午10:00在A處測得燈塔C位于輪船的北偏西30°方向,上午10:40在B處測得燈塔C位于輪船的北偏東60°方向,且與燈塔C相距12km.
(1)若輪船照此速度與航向航向,何時到達海岸線?
(2)若輪船不改變航向,該輪船能否停靠在碼頭?請說明理由(參考數據: ![]() ≈1.4,
≈1.4, ![]() ≈1.7).
≈1.7).

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在△ABC中,AB=![]() ,BC=6,∠B=45°,D為BC邊上一點將△ABC沿著過D點的直線折疊,使得點C落在AB邊上,記CD=m,則AC=_____,m的取值范圍是_____
,BC=6,∠B=45°,D為BC邊上一點將△ABC沿著過D點的直線折疊,使得點C落在AB邊上,記CD=m,則AC=_____,m的取值范圍是_____
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了掌握八年級數學考試卷的命題質量與難度系數,命題組教師赴外地選取一個水平相當的八年級班級進行預測,將考試成績分布情況進行處理分析,制成頻數分布表如下(成績得分均為整數):
組別 | 成績分組 | 頻數頻率 | 頻數 |
1 |
| 2 | 0.05 |
2 |
| 4 | 0.10 |
3 |
|
| 0.2 |
4 |
| 10 | 0.25 |
5 |
|
|
|
6 |
| 6 | 0.15 |
合計 | 40 | 1.00 |
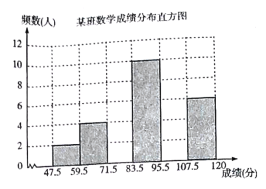
根據表中提供的信息解答下列問題:
(1)頻數分布表中的![]() ,
,![]() ,
,![]() ;
;
(2)已知全區八年級共有200個班(平均每班40人),用這份試卷檢測,108分及以上為優秀,預計優秀的人數約為 ,72分及以上為及格,預計及格的人數約為 ,及格的百分比約為 ;
(3)補充完整頻數分布直方圖.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】中華文化源遠流長,文學方面,《西游記》、《三國演義》、《水滸傳》、《紅樓夢》是我國古代長篇小說中的典型代表,被稱為“四大古典名著”某中學為了解學生對四大名著的閱讀情況,就“四大古典名著你讀完了幾部”的問題在全校學生中進行了抽樣調查,根據調查結果繪制成如下尚不完整的統計圖.
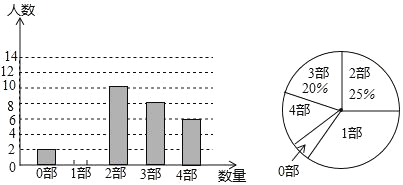
請根據以上信息,解決下列問題
(1)本次調查所得數據的眾數是____部,中位數是_____部;
(2)扇形統計圖中“4部”所在扇形的圓心角為_____度;
(3)請將條形統計圖補充完整;
(4)沒有讀過四大古典名著的兩名學生準備從中各自隨機選擇一部來閱讀,求他們恰好選中同一名著的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
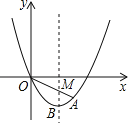
【題目】已知:如圖,在平面直角坐標系xOy中,拋物線y=ax2+bx(a≠0)經過點A(6,﹣3),對稱軸是直線x=4,頂點為B,OA與其對稱軸交于點M,M、N關于點B對稱.
(1)求這條拋物線的表達式和點B的坐標;
(2)聯結ON、AN,求△OAN的面積;
(3)點Q在x軸上,且在直線x=4右側,當∠ANQ=45°時,求點Q的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在“優秀傳統文化進校園”活動中,學校計劃每周二下午第三節課時間開展此項活動,擬開展活動項目為:剪紙,武術,書法,器樂,要求七年級學生人人參加,并且每人只能參加其中一項活動.教務處在該校七年級學生中隨機抽取了100名學生進行調查,并對此進行統計,繪制了如圖所示的條形統計圖和扇形統計圖(均不完整).
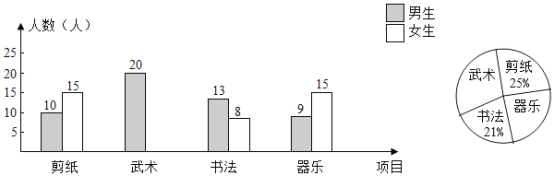
請解答下列問題:
(1)請補全條形統計圖和扇形統計圖;
(2)在參加“剪紙”活動項目的學生中,男生所占的百分比是多少?
(3)若該校七年級學生共有500人,請估計其中參加“書法”項目活動的有多少人?
(4)學校教務處要從這些被調查的女生中,隨機抽取一人了解具體情況,那么正好抽到參加“器樂”活動項目的女生的概率是多少?

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com