
【題目】如圖,已知一次函數![]() 的圖像與x軸交于A(-6,0)與y軸相交于點B,動點P從A出發,沿x軸向x軸的正方向運動.
的圖像與x軸交于A(-6,0)與y軸相交于點B,動點P從A出發,沿x軸向x軸的正方向運動.
(1)求b的值,并求出△PAB為等腰三角形時點P的坐標;
(2)在點P出發的同時,動點Q也從點A出發,以每秒![]() 個單位的速度,沿射線AB運動,運動時間為t(s);
個單位的速度,沿射線AB運動,運動時間為t(s);
①點Q的坐標(用含t的表達式表示);
②若點P的運動速度為每秒k個單位,請直接寫出當△APQ為等腰三角形時k的值.

【答案】(1)解:![]() 當
當![]() 為等腰三角形時點
為等腰三角形時點 ![]() 的坐標為:
的坐標為:![]() 或
或![]() 或
或![]() ;(2)①
;(2)①![]() ,②
,②![]() 的值分別為:
的值分別為:![]() 、6、
、6、![]() .
.
【解析】
(1)利用待定系數法把點A坐標代入一次函數解析式,即可求出b的值;若![]() ,需分
,需分![]() 、
、![]() 、
、![]() 三種情況分類討論;
三種情況分類討論;
(2)①設Q點橫坐標為a,因為Q點在射線AB上,所以橫坐標為![]() ,即
,即![]() ,作
,作 ![]() 軸于點
軸于點 ![]() ,則
,則 ![]() ,
,![]() ,所以
,所以![]() ,又因為
,又因為![]() ,所以
,所以![]() ,解得
,解得![]() ,表示出
,表示出![]() .②AP=tk,分AP=AQ,AP=PQ,AQ=AP三種情況即可解答,
.②AP=tk,分AP=AQ,AP=PQ,AQ=AP三種情況即可解答,
(1)解:把 ![]() ,
,![]() 代入
代入 ![]() 得:
得:![]() .
.
∴![]() ,
,![]() ,
,![]() ,
,![]() .
.
當![]() 時,
時,![]() .∴
.∴![]() ;
;
當![]() 時,
時,![]() .∴
.∴![]() ;
;
當 ![]() 時,設
時,設 ![]() ,則
,則 ![]() ,
,
在 ![]() 中,由
中,由 ![]() 可得:
可得:![]() .
.
∴![]() ;
;
綜上,當![]() 為等腰三角形時點
為等腰三角形時點 ![]() 的坐標為:
的坐標為:![]() 或
或![]() 或
或![]() .
.
(2)①解:設![]() ,作
,作 ![]() 軸于點
軸于點 ![]() ,
,
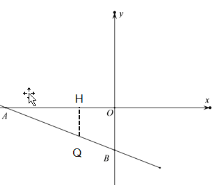
則 ![]() ,
,![]() ,∴
,∴![]() .
.
又∵![]() ,∴
,∴![]() ,∴
,∴![]() , ∴
, ∴![]() .
.
②![]() 的值分別為:
的值分別為:![]() 、6、
、6、![]() .
.


科目:初中數學 來源: 題型:
【題目】如圖,四邊形ABCD中,AB∥CD,BC⊥CD,E是AD的中點,連結BE并延長交CD的延長線于點F.

(1)請連結AF、BD,試判斷四邊形ABDF是何種特殊四邊形,并說明理由.
(2)若AB=4,BC=5,CD=6,求△BCF的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,∠ABC=90°,D是邊AC上一點,連接BD,使∠A=2∠1,點E是BC上的一點,以BE為直徑的⊙O經過點D.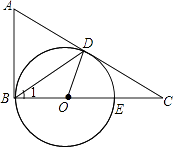
(1)求證:AC是⊙O的切線;
(2)若∠A=60°,⊙O的半徑為2,求AB的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某農戶以1500元/畝的單價承包了15畝地種植板栗,每畝種植80株優質板栗嫁接苗,購買嫁接苗,購買價格為5元/株,且每畝地的管理費用為800元,一年下來喜獲豐收平均每畝板栗產量為600kg,已知當地板栗的批發和;零售價格分別如下表所示:
銷售方式 | 批發 | 零售 |
售價(元/kg) | 10 | 14 |
通過市場調研發現,批發與零售的總銷量只能達到總產量的70%,其中零售量不高于總銷售量的40%,經多方協調當地食品加工廠承諾以7元/kg的價格收購該農戶余下的板栗,設板栗全部售出后的總利潤為y元,其中零售x kg.
(1)求y與x之間的函數關系
(2)求該農戶所收獲的最大利潤
(總利潤=總銷售額-總承包費用-購買板栗苗的費用-總管理費用)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】南沙群島是我國固有領土,現在我南海漁民要在南沙某海島附近進行捕魚作業,當漁船航行至B處時,測得該島位于正北方向20(1+ ![]() )海里的C處,為了防止某國海巡警干擾,就請求我A處的漁監船前往C處護航,已知C位于A處的北偏東45°方向上,A位于B的北偏西30°的方向上,求A、C之間的距離.
)海里的C處,為了防止某國海巡警干擾,就請求我A處的漁監船前往C處護航,已知C位于A處的北偏東45°方向上,A位于B的北偏西30°的方向上,求A、C之間的距離.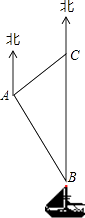
查看答案和解析>>
科目:初中數學 來源: 題型:
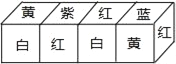
【題目】把正方體的6個面分別涂上不同的顏色,并畫上朵數不等的花,各面上的顏色與花朵數的情況如下表:
顏色 | 紅 | 黃 | 藍 | 白 | 紫 | 綠 |
花朵數 | 1 | 2 | 3 | 4 | 5 | 6 |
現將上述大小相同,顏色、花朵分布完全一樣的四個正方體拼成一個在同一平面上放置的長方體,如圖所示,那么長方體的下底面共有_____朵花.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】等腰三角形ABC在平面直角坐標系中的位置如圖所示,已知點A(﹣6,0),點B在原點,CA=CB=5,把等腰三角形ABC沿x軸正半軸作無滑動順時針翻轉,第一次翻轉到位置①,第二次翻轉到位置②…依此規律,第15次翻轉后點C的橫坐標是 . 
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,一次函數y=-![]() x+3
x+3![]() 的圖像分別與x軸、y軸交于A、B兩點.動點P從A點開始沿折線AO-OB-BA運動,點P在AO,OB,BA上運動的速度分別為1,
的圖像分別與x軸、y軸交于A、B兩點.動點P從A點開始沿折線AO-OB-BA運動,點P在AO,OB,BA上運動的速度分別為1,![]() ,2 (長度單位/秒);動點E從O點開始以
,2 (長度單位/秒);動點E從O點開始以![]() (長度單位/秒)的速度沿線段OB運動.設P、E兩點同時出發,運動時間為t (秒),當點P沿折線AO-OB-BA運動一周時,動點E和P同時停止運動.過點E作EF∥OA,交AB于點F.
(長度單位/秒)的速度沿線段OB運動.設P、E兩點同時出發,運動時間為t (秒),當點P沿折線AO-OB-BA運動一周時,動點E和P同時停止運動.過點E作EF∥OA,交AB于點F.
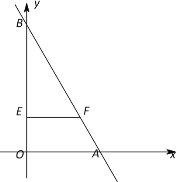
(1)求線段AB的長;
(2)求證:∠ABO=30°;
(3)當t為何值時,點P與點E重合?
(4)當t = 時,PE=PF .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com