
【題目】已知關于![]() 的方程
的方程![]() 有兩個正整數根(
有兩個正整數根(![]() 是正整數).
是正整數).![]() 的三邊
的三邊![]() 、
、![]() 、
、![]() 滿足
滿足![]() ,
,![]() ,
,![]() .
.
求:
![]() 的值;
的值;
![]() 的面積.
的面積.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() .
.
【解析】
(1)已知關于![]() 的方程
的方程![]() 有兩個正整數根(
有兩個正整數根(![]() 是整數),由此即可得
是整數),由此即可得![]() ,設
,設![]() ,
,![]() 是此方程的兩個根,根據根與系數的關系可得
是此方程的兩個根,根據根與系數的關系可得![]() ,因為
,因為![]() 也是正整數,即可得
也是正整數,即可得![]() 或
或![]() 或
或![]() 或
或![]() 或
或![]() 或
或![]() ,再由
,再由![]() 為正整數,即可得
為正整數,即可得![]() ;(2)由(1)得出的m的值,然后將
;(2)由(1)得出的m的值,然后將![]() ,
,![]() 進行化簡,得出a,b的值.然后再根據三角形三邊的關系來確定符合條件的a,b的值,進而得出三角形的面積.
進行化簡,得出a,b的值.然后再根據三角形三邊的關系來確定符合條件的a,b的值,進而得出三角形的面積.
![]() ∵關于
∵關于![]() 的方程
的方程![]() 有兩個正整數根(
有兩個正整數根(![]() 是整數).
是整數).
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
設![]() ,
,![]() 是此方程的兩個根,
是此方程的兩個根,
∴![]() ,
,
∴![]() 也是正整數,即
也是正整數,即![]() 或
或![]() 或
或![]() 或
或![]() 或
或![]() 或
或![]() ,
,
又![]() 為正整數,
為正整數,
∴![]() ;
;
![]() 把
把![]() 代入兩等式,化簡得
代入兩等式,化簡得![]() ,
,![]()
當![]() 時,
時,![]()
當![]() 時,
時,![]() 、
、![]() 是方程
是方程![]() 的兩根,而
的兩根,而![]() ,由韋達定理得
,由韋達定理得![]() ,
,![]() ,則
,則![]() 、
、![]() .
.
①![]() ,
,![]() 時,由于
時,由于![]()
故![]() 為直角三角形,且
為直角三角形,且![]() ,
,![]() .
.
②![]() ,
,![]() 時,因
時,因![]() ,故不能構成三角形,不合題意,舍去.
,故不能構成三角形,不合題意,舍去.
③![]() ,
,![]() 時,因
時,因![]() ,故能構成三角形.
,故能構成三角形.
![]()
綜上,![]() 的面積為
的面積為![]() 或
或![]() .
.


 心算口算巧算一課一練系列答案
心算口算巧算一課一練系列答案 應用題作業本系列答案
應用題作業本系列答案科目:初中數學 來源: 題型:
【題目】已知關于x的一元二次方程![]() 有實數根.
有實數根.
(1)求m的值;
(2)先作![]() 的圖象關于x軸的對稱圖形,然后將所作圖形向左平移3個單位長度,再向上平移2個單位長度,寫出變化后圖象的解析式;
的圖象關于x軸的對稱圖形,然后將所作圖形向左平移3個單位長度,再向上平移2個單位長度,寫出變化后圖象的解析式;
(3)在(2)的條件下,當直線y=2x+n(n≥m)與變化后的圖象有公共點時,求![]() 的最大值和最小值.
的最大值和最小值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,已知點![]() ,
,![]() 與坐標原點O在同一直線上,且AO=BO,其中m,n滿足
與坐標原點O在同一直線上,且AO=BO,其中m,n滿足![]() .
.
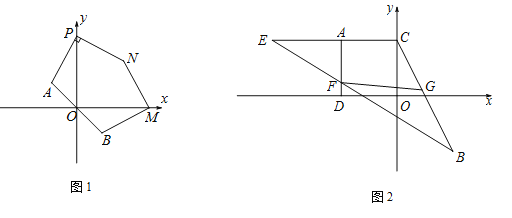
(1)求點A,B的坐標;
(2)如圖1,若點M,P分別是x軸正半軸和y軸正半軸上的點,點P的縱坐標不等于2,點N在第一象限內,且![]() ,PA⊥PN,
,PA⊥PN,![]() ,求證:BM⊥MN;
,求證:BM⊥MN;
(3)如圖2,作AC⊥y軸于點C,AD⊥x軸于點D,在CA延長線上取一點E,使![]() ,連結BE交AD于點F,恰好有
,連結BE交AD于點F,恰好有![]() ,點G是CB上一點,且
,點G是CB上一點,且![]() ,連結FG,求證:
,連結FG,求證:![]() .
.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某氣球內充滿一定質量的氣體,當溫度不變時,氣球內氣體的氣壓p(kPa)是氣體體積V(m3)的反比例函數,其圖象如圖所示.

(1)寫出這一函數的表達式.
(2)當氣體體積為1 m3時,氣壓是多少?
(3)當氣球內的氣壓大于140 kPa時,氣球將爆炸,為了安全考慮,氣體的體積應不小于多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,在矩形ABCD中,點A(1,1),B(3,1),C(3,2),反比例函數y=![]() (x>0)的圖象經過點D,且與AB相交于點E,
(x>0)的圖象經過點D,且與AB相交于點E,
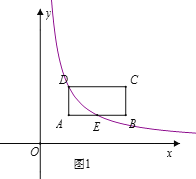
(1)求反比例函數的解析式;
(2)過點C、E作直線,求直線CE的解析式;
(3)如圖2,將矩形ABCD沿直線CE平移,使得點C與點E重合,求線段BD掃過的面積.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AD是△ABC的高線,BD=CD,點E是AD上一點,BE=BC,將△ABE沿BE所在直線折疊,點A落在點A′位置上,連接AA',BA′,EA′與AC相交于點H,BA′與AC相交于點F.小夏依據上述條件,寫出下列四個結論:①∠EBC=60°;②∠BFC=60°;③∠EA′A=60°;④∠A′HA=60°.以上結論中,正確的是( )

A.①B.③④C.①②③D.①②④
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知矩形![]() 的邊長
的邊長![]() .某一時刻,動點
.某一時刻,動點![]() 從
從![]() 點出發沿
點出發沿![]() 方向以
方向以![]() 的速度向
的速度向![]() 點勻速運動;同時,動點
點勻速運動;同時,動點![]() 從
從![]() 點出發沿
點出發沿![]() 方向以
方向以![]() 的速度向
的速度向![]() 點勻速運動,問:
點勻速運動,問:

(1)經過多少時間,![]() 的面積等于矩形
的面積等于矩形![]() 面積的
面積的![]() ?
?
(2)是否存在時刻t,使以A,M,N為頂點的三角形與![]() 相似?若存在,求t的值;若不存在,請說明理由.
相似?若存在,求t的值;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,已知△ABC的三個頂點坐標分別是A(1,1),B(4,1),C(3,3).
(1)將△ABC向下平移5個單位后得到△A1B1C1,請畫出△A1B1C1;
(2)將△ABC繞原點O逆時針旋轉90°后得到△A2B2C2,請畫出△A2B2C2;
(3)判斷以O,A1,B為頂點的三角形的形狀.(無須說明理由)

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com