
【題目】如圖,![]() 是
是![]() 的直徑,
的直徑,![]() 為
為![]() 的弦,
的弦,![]() ,
,![]() 與
與![]() 的延長線交于點
的延長線交于點![]() ,點
,點![]() 在
在![]() 上, 滿足
上, 滿足![]() .
.
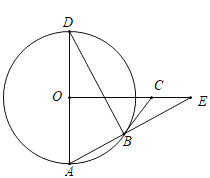
(1)求證:![]() 是
是![]() 的切線;
的切線;
(2)若![]() ,
,![]() , 求線段
, 求線段![]() 的長.
的長.
【答案】(1)見解析;(2)![]() .
.
【解析】
(1)連接OB,如圖,根據圓周角定理得到∠ABD=90°,再根據等腰三角形的性質和已知條件證出∠OBC=90°,即可得出結論;
(2)根據圓周角定理得到∠ABD=90°,得到∠A=60°,求得∠E=30°,根據等腰三角形的性質得到CE=CB,根據三角形外角的性質得到∠BCO=60°,解直角三角形即可得到結論.
(1)證明:連接OB,如圖,
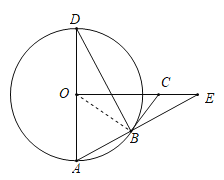
∵AD是⊙O的直徑,
∴∠ABD=90°,
∴∠A+∠ADB=90°,
∵OA=OB,
∴∠A=∠OBA,
∵∠CBE=∠ADB,
∴∠OBA+∠CBE=90°,
∴∠OBC=180°-90°=90°,
∴BC⊥OB,
∴BC是⊙O的切線;
(2)∵AD是⊙O的直徑,
∴∠ABD=90°,
∴∠A=60°,
∵OE⊥AD,
∴∠AOE=90°,
∴∠E=30°,
∵∠CBE=30°,
∴∠CBE=∠E=30°,
∴CE=CB,
∴∠BCO=60°,
在![]() 中
中
![]()
![]()
∴BC=![]() OB=
OB=![]() ,
,
∴CE=![]() .
.


 期末沖刺100分創新金卷完全試卷系列答案
期末沖刺100分創新金卷完全試卷系列答案科目:初中數學 來源: 題型:
【題目】小吳家準備購買一臺電視機,小吳將收集到的某地區A、B、C三種品牌電視機銷售情況的有關數據統計如下:
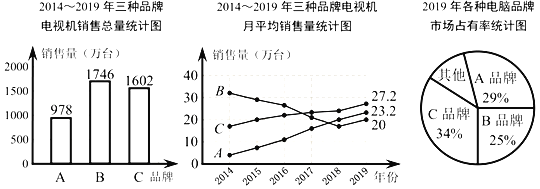
根據上述三個統計圖,請解答:
(1)2014~2019年三種品牌電視機銷售總量最多的是 品牌,月平均銷售量最穩定的是 品牌.
(2)2019年其他品牌的電視機年銷售總量是多少萬臺?
(3)貨比三家后,你建議小吳家購買哪種品牌的電視機?說說你的理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】若二次函數![]() 的圖象與
的圖象與![]() 軸分別交于點
軸分別交于點![]() 、
、![]() ,且過點
,且過點![]() .
.
(1)求二次函數表達式;
(2)若點![]() 為拋物線上第一象限內的點,且
為拋物線上第一象限內的點,且![]() ,求點
,求點![]() 的坐標;
的坐標;
(3)在拋物線上(![]() 下方)是否存在點
下方)是否存在點![]() ,使
,使![]() ?若存在,求出點
?若存在,求出點![]() 到
到![]() 軸的距離;若不存在,請說明理由.
軸的距離;若不存在,請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,濟南市為加快![]() 網絡建設,某通信公司在一個坡度為
網絡建設,某通信公司在一個坡度為![]() 的山腰上建了一座垂直于水平面的
的山腰上建了一座垂直于水平面的![]() 信號通信塔
信號通信塔![]() ,在距山腳
,在距山腳![]() 處水平距離
處水平距離![]() 的點
的點![]() 處測得通信塔底
處測得通信塔底![]() 處的仰角是
處的仰角是![]() ,通信塔頂
,通信塔頂![]() 處的仰角是
處的仰角是![]() .則通信塔的高度
.則通信塔的高度![]() 為( )(結果保留整數,參考數據:
為( )(結果保留整數,參考數據:![]() ,
,![]() )
)

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
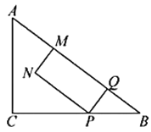
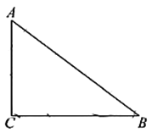
【題目】如圖,在![]() 中,
中,![]() ,
,![]() ,
,![]() .點
.點![]() 從點
從點![]() 出發,以每秒5個單位長度的速度沿
出發,以每秒5個單位長度的速度沿![]() 向終點
向終點![]() 運動,同時點
運動,同時點![]() 從點
從點![]() 出發,以相同的速度沿
出發,以相同的速度沿![]() 向終點
向終點![]() 運動,過點
運動,過點![]() 作
作![]() 于點
于點![]() ,連結
,連結![]() ,以
,以![]() 、
、![]() 為鄰邊作矩形
為鄰邊作矩形![]() ,當點
,當點![]() 運動到終點時,整個運動停止,設矩形
運動到終點時,整個運動停止,設矩形![]() 與
與![]() 重疊部分圖形的面積為
重疊部分圖形的面積為![]() ,點
,點![]() 的運動時間為
的運動時間為![]() 秒.
秒.
(1)①![]() 的長為 ;
的長為 ;
②用含![]() 的代數式表示線段
的代數式表示線段![]() 的長為 ;
的長為 ;
(2)當![]() 的長度為10時,求
的長度為10時,求![]() 的值;
的值;
(3)求![]() 與
與![]() 的函數關系式;
的函數關系式;
(4)當過點![]() 和點
和點![]() 的直線垂直于
的直線垂直于![]() 的一邊時,直接寫出
的一邊時,直接寫出![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】隨著![]() 技術的發展,人們對各類
技術的發展,人們對各類![]() 產品的使用充滿期待.某公司計劃在某地區銷售第一款
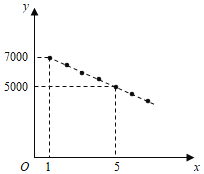
產品的使用充滿期待.某公司計劃在某地區銷售第一款![]() 產品,根據市場分析,該產品的銷售價格將隨銷售周期的變化而變化.設該產品在第
產品,根據市場分析,該產品的銷售價格將隨銷售周期的變化而變化.設該產品在第![]() (
(![]() 為正整數)個銷售周期每臺的銷售價格為
為正整數)個銷售周期每臺的銷售價格為![]() 元,
元,![]() 與
與![]() 之間滿足如圖所示的一次函數關系.
之間滿足如圖所示的一次函數關系.
(1)求![]() 與
與![]() 之間的關系式;
之間的關系式;
(2)設該產品在第![]() 個銷售周期的銷售數量為
個銷售周期的銷售數量為![]() (萬臺),
(萬臺),![]() 與
與![]() 的關系可用
的關系可用![]() 來描述.根據以上信息,試問:哪個銷售周期的銷售收入最大?此時該產品每臺的銷售價格是多少元?
來描述.根據以上信息,試問:哪個銷售周期的銷售收入最大?此時該產品每臺的銷售價格是多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
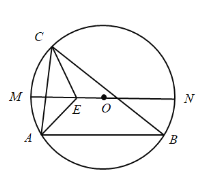
【題目】如圖,![]() 是
是![]() 的直徑,弦
的直徑,弦![]() 點
點![]() 是直徑
是直徑![]() 上方半圓上的動點(包括端點
上方半圓上的動點(包括端點![]() 和
和![]() 的平分線相交于點E,當點
的平分線相交于點E,當點![]() 從點
從點![]() 運動到點
運動到點![]() 時,則
時,則![]() 兩點的運動路徑長的比值是( )
兩點的運動路徑長的比值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com