
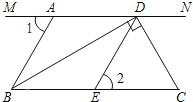
【題目】如圖,MN∥BC,BD⊥DC,∠1=∠2=60°.
(1)AB 與 DE 平行嗎?請說明理由;
(2)若 DC 是∠NDE 的平分線.
①試說明∠ABC=∠C;
②試說明 BD 是∠ABC 的平分線.
【答案】(1)AB∥DE,理由見解析;(2)見解析.
【解析】(1)首先根據平行線的性質,兩直線平行,內錯角相等即可證得∠ABC=∠1=60°,進而證明∠ABC=∠2,根據同位角相等,兩直線平行,即可證得;
(2)①根據平行線的性質,兩直線平行,同旁內角互補求得∠NDE的度數,然后根據角平分線的定義,以及平行線的性質即可求得∠C的度數,從而判斷;
②在直角△BCD中,求得∠DBC的度數,然后求得∠ABD的度數,即可證得.
(1)AB∥DE,理由如下:
∵MN∥BC( 已知 ),
∴∠ABC=∠1=60°( 兩直線平行,內錯角相等 ).
又∵∠1=∠2( 已知 ).
∴∠ABC=∠2( 等量代換 ).
∴AB∥DE( 同位角相等,兩直線平行 );
(2)①∵MN∥BC,
∴∠NDE+∠2=180°,
∴∠NDE=180°﹣∠2=180°﹣60°=120°.
∵DC 是∠NDE 的平分線,
∴∠EDC=∠NDC=![]() ∠NDE=60°.
∠NDE=60°.
∵MN∥BC,
∴∠C=∠NDC=60°.
∴∠ABC=∠C.
②∠ADC=180°﹣∠NDC=180°﹣60°=120°,
∵BD⊥DC,
∴∠BDC=90°.
∴∠ADB=∠ADC﹣∠BDC=120°﹣90°=30°.
∵MN∥BC,
∴∠DBC=∠ADB=30°.
∴∠ABD=∠DBC=![]() ∠ABC.
∠ABC.
∴BD 是∠ABC 的平分線.


科目:初中數學 來源: 題型:
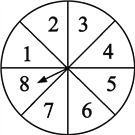
【題目】如圖所示,轉盤被等分成八個扇形,并在上面依次標有數字1,2,3,4,5,6,7,8.
(1)自由轉動轉盤,當它停止轉動時,指針指向的數正好能整除8的概率是多少?
(2)請你用這個轉盤設計一個游戲,當自由轉動的轉盤停止時,指針指向的區域的概率為![]() .(注:指針指在邊緣處,要重新轉,直至指到非邊緣處)
.(注:指針指在邊緣處,要重新轉,直至指到非邊緣處)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某單位有職工200人,其中青年職工(20﹣35歲),中年職工(35﹣50歲),老年職工(50歲及 以上)所占比例如扇形統計圖所示. 為了解該單位職工的健康情況,小張、小王和小李各自對單位職工進行了抽樣調查,將收集的數據進行了整理,繪制的統計表分別為表1、表2和表3.
表1:小張抽樣調查單位3名職工的健康指數
年齡 | 26 | 42 | 57 |
健康指數 | 97 | 79 | 72 |
表2:小王抽樣調查單位10名職工的健康指數
年齡 | 23 | 25 | 26 | 32 | 33 | 37 | 39 | 42 | 48 | 52 |
健康指數 | 93 | 89 | 90 | 83 | 79 | 75 | 80 | 69 | 68 | 60 |
表3:小李抽樣調查單位10名職工的健康指數
年齡 | 22 | 29 | 31 | 36 | 39 | 40 | 43 | 46 | 51 | 55 |
健康指數 | 94 | 90 | 88 | 85 | 82 | 78 | 72 | 76 | 62 | 60 |
根據上述材料回答問題:
(1)小張、小王和小李三人中,誰的抽樣調查的數據能夠較好地反映出該單位職工健康情況,并簡要說明其他兩位同學抽樣調查的不足之處.
(2)根據能夠較好地反映出該單位職工健康情況表,繪制出青年職工、中年職工、老年職工健康指數的平均數的直方圖.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖①,四邊形ABCD中,BC∥AD,∠A=90°,點P從A點出發,沿折線AB→BC→CD運動,到點D時停止,已知△PAD的面積s與點P運動的路程x的函數圖象如圖②所示,則點P從開始到停止運動的總路程為( )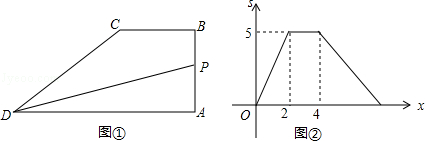
A.4
B.2+ ![]()
C.5
D.4+ ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一副直角三角尺疊放如圖 1 所示,現將 45°的三角尺ADE 固定不動,將含 30°的三角尺 ABC 繞頂點 A 順時針轉動(旋轉角不超過 180 度),使兩塊三角尺至少有一組邊互相平行.如圖 2:當∠BAD=15°時,BC∥DE.則∠BAD(0°<∠BAD<180°)其它所有可能符合條件的度數為________.

查看答案和解析>>
科目:初中數學 來源: 題型:
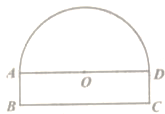
【題目】如圖,隧道的截面由半圓和長方形構成,長方形的長BC為8m,寬AB為1m,該隧道內設雙向行駛的車道(共有2條車道),若現有一輛貨運卡車高4m,寬2.3m。則這輛貨運卡車能否通過該隧道?說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系xOy中,矩形OEFG的頂點E的坐標為(4,0),頂點G的坐標為(0,2),將矩形OEFG繞點O逆時針旋轉,使點F落在y軸的點N處,得到矩形OMNP,OM與GF交于點A.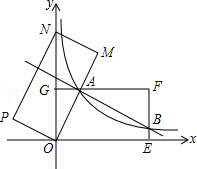
(1)求圖象經過點A的反比例函數的解析式;
(2)設(2)中的反比例函數圖象交EF于點B,直接寫出直線AB的解析式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠BAC=90°,∠C=30°,以邊上AC上一點O為圓心,OA為半徑作⊙O,⊙O恰好經過邊BC的中點D,并與邊AC相交于另一點F. 
(1)求證:BD是⊙O的切線.
(2)若AB= ![]() ,E是半圓
,E是半圓 ![]() 上一動點,連接AE,AD,DE. 填空:
上一動點,連接AE,AD,DE. 填空:
①當 ![]() 的長度是時,四邊形ABDE是菱形;
的長度是時,四邊形ABDE是菱形;
②當 ![]() 的長度是時,△ADE是直角三角形.
的長度是時,△ADE是直角三角形.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com