【題目】小強擲兩枚質地均勻的骰子，每個骰子的六個面上分別刻有1到6的點數，則兩枚骰子點數相同的概率為
【答案】
【解析】解：列表得：
（1，6） | （2，6） | （3，6） | （4，6） | （5，6） | （6，6） |
（1，5） | （2，5） | （3，5） | （4，5） | （5，5） | （6，5） |
（1，4） | （2，4） | （3，4） | （4，4） | （5，4） | （6，4） |
（1，3） | （2，3） | （3，3） | （4，3） | （5，3） | （6，3） |
（1，2） | （2，2） | （3，2） | （4，2） | （5，2） | （6，2） |
（1，1） | （2，1） | （3，1） | （4，1） | （5，1） | （6，1） |
由表可知一共有36種情況，兩枚骰子點數相同的有6種，
所以兩枚骰子點數相同的概率= 
= ，
故答案為： ．
首先根據題意列出表格，然后由表格即可求得所有等可能的結果與兩枚骰子點數相同的情況，再利用概率公式即可求得答案．
開心蛙口算題卡系列答案科目：初中數學 來源： 題型：
【題目】如圖，在平面直角坐標系中，A(1，2)，B(3，1)，C(-2，-1).
（1）在圖中作出
關于
軸對稱的
.
（2）寫出點
的坐標（直接寫答案）.
A1_____________，B1______________，C1______________
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】從﹣3，﹣1，0，1，3這五個數中隨機抽取一個數記為a，再從剩下的四個數中任意抽取一個數記為b，恰好使關于x，y的二元一次方程組 
有整數解，且點（a，b）落在雙曲線 
上的概率是 ．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，△ABC和△DEC都是等腰直角三角形，C為它們的公共直角頂點，連AD，BE，F為線段AD的中點，連接CF
（1）如圖1，當D點在BC上時，求證：①BE=2CF，②BE⊥CF．
（2）如圖2，把△DEC繞C點順時針旋轉一個銳角，其他條件不變，問（1）中的關系是否仍然成立？如果成立請證明．如果不成立，請寫出相應的正確的結論并加以證明．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在正方形ABCD（四個邊相等，四個角為直角）中，E，F分別為AD，BC的中點，P為對角線BD上的一個動點，則下列線段的長等于AP+EP最小值的是( )
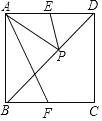
A. AB B. DE C. AF D. BD
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在平面直角坐標系中，點O為坐標原點，△ABC是直角三角形，∠ACB=90°，點B、C都在第一象限內，CA⊥x軸，垂足為點A，反比例函數y1= 
的圖象經過點B；反比例函數y2= 
的圖象經過點C（ 
，m）．
（1）求點B的坐標；
（2）△ABC的內切圓⊙M與BC，CA，AB分別相切于D，E，F，求圓心M的坐標．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】暑假期間，某學校計劃用彩色的地面磚鋪設教學樓門前一塊矩形操場ABCD的地面．已知這個矩形操場地面的長為100m，寬為80m，圖案設計如圖所示：操場的四角為小正方形，陰影部分為四個矩形，四個矩形的寬都為小正方形的邊長，在實際鋪設的過程總，陰影部分鋪紅色地面磚，其余部分鋪灰色地面磚． 
（1）如果操場上鋪灰色地面磚的面積是鋪紅色地面磚面積的4倍，那么操場四角的每個小正方形邊長是多少米？
（2）如果灰色地面磚的價格為每平方米30元，紅色地面磚的價格為每平方米20元，學校現有15萬元資金，問這些資金是否能購買所需的全部地面磚？如果能購買所學的全部地面磚，則剩余資金是多少元？如果不能購買所需的全部地面磚，教育局還應該至少給學校解決多少資金？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某物流公司引進A、B兩種機器人用來搬運某種貨物，這兩種機器人充滿電后可以連續搬運5小時，A種機器人于某日0時開始搬運，過了1小時，B種機器人也開始搬運，如圖，線段OG表示A種機器人的搬運量yA（千克）與時間x（時）的函數圖象，根據圖象提供的信息，解答下列問題：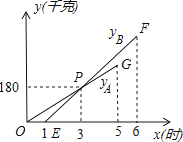
（1）求yB關于x的函數解析式；
（2）如果A、B兩種機器人連續搬運5個小時，那么B種機器人比A種機器人多搬運了多少千克？
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
