
【題目】平面直角坐標(biāo)系xOy中,對(duì)于點(diǎn)P(a,b),若點(diǎn)P′的坐標(biāo)為(a ![]() ,ka+b)(其中k為常數(shù),且k≠0),則稱(chēng)點(diǎn)P′為點(diǎn)P的“k關(guān)聯(lián)點(diǎn)”.
,ka+b)(其中k為常數(shù),且k≠0),則稱(chēng)點(diǎn)P′為點(diǎn)P的“k關(guān)聯(lián)點(diǎn)”.
(1)求點(diǎn)P(﹣2,3)的“2關(guān)聯(lián)點(diǎn)”P(pán)′的坐標(biāo);
(2)若a、b為正整數(shù),點(diǎn)P的“k關(guān)聯(lián)點(diǎn)”P(pán)′的坐標(biāo)為(3,6),求出k及點(diǎn)P的坐標(biāo);
(3)如圖,點(diǎn)Q的坐標(biāo)為(0,4 ![]() ),點(diǎn)A在函數(shù)y=﹣
),點(diǎn)A在函數(shù)y=﹣ ![]() (x<0)的圖象上運(yùn)動(dòng),且點(diǎn)A是點(diǎn)B的“﹣
(x<0)的圖象上運(yùn)動(dòng),且點(diǎn)A是點(diǎn)B的“﹣ ![]() 關(guān)聯(lián)點(diǎn)”,當(dāng)線段BQ最短時(shí),求B點(diǎn)坐標(biāo).
關(guān)聯(lián)點(diǎn)”,當(dāng)線段BQ最短時(shí),求B點(diǎn)坐標(biāo).
【答案】
(1)解:∵x=﹣2+ ![]() =﹣
=﹣ ![]() ,y=2×(﹣2)+3=﹣1,
,y=2×(﹣2)+3=﹣1,
∴P′(﹣ ![]() ,﹣1);
,﹣1);
(2)解:設(shè)P(a,b),則P′(a ![]() ,ka+b)
,ka+b)
∴  ,
,
∴k=2,
∴2a+b=6.
∵a、b為正整數(shù)
∴P′(1,4)、(2,2);
(3)解:∵B的“﹣ ![]() 關(guān)聯(lián)點(diǎn)”是A,
關(guān)聯(lián)點(diǎn)”是A,
∴A(a﹣ ![]() ,﹣
,﹣ ![]() a+b),
a+b),
∵點(diǎn)A還在反比例函數(shù)y=﹣ ![]() 的圖象上,
的圖象上,
∴(﹣ ![]() a+b)(a﹣
a+b)(a﹣ ![]() )=﹣4
)=﹣4 ![]() ,
,
∴(b﹣ ![]() a)2=12,
a)2=12,
∵b﹣ ![]() a>0,
a>0,
∴b﹣ ![]() a=2
a=2 ![]() ,
,
∴b= ![]() a+2
a+2 ![]() ;
;
∴B在直線y= ![]() x+2
x+2 ![]() 上.
上.
過(guò)Q作y= ![]() x+2
x+2 ![]() 的垂線QB1,垂足為B1,
的垂線QB1,垂足為B1, 
∵Q(0,4 ![]() ),且線段BQ最短,
),且線段BQ最短,
∴B1即為所求的B點(diǎn),
由△MB1Q∽△MON 得 ![]() ,
,
∵ON=2,OM=2 ![]() ,
,
∴MN=4.
又∵M(jìn)Q=2 ![]() ,
,
∴B1Q= ![]() ,MB1=3
,MB1=3
在Rt△MB1Q中,B1QMB1=MQhB1,
∴hB1= ![]() ,
,
∴xB1= ![]() ,
,
∴B( ![]() ,
, ![]()
![]() ).
).
【解析】(1)根據(jù)新定義求出P′的坐標(biāo)。
(2)根據(jù)新定義,建立方程組,就可以求出k及點(diǎn)P的坐標(biāo)。
(3)根據(jù)題意表示出點(diǎn)A的坐標(biāo),再代入反比例函數(shù)求得b的值,從而求得點(diǎn)B在一次函數(shù)圖像上,過(guò)Q作y= ![]() x+2
x+2 ![]() 的垂線QB1,垂足為B1, 則線段BQ最短,B1即為所求的B點(diǎn),然后由△MB1Q∽△MON 得對(duì)應(yīng)邊成比例,求出MN、B1Q、MB1的長(zhǎng),再利用三角形的面積公式即可求出點(diǎn)B的坐標(biāo)。
的垂線QB1,垂足為B1, 則線段BQ最短,B1即為所求的B點(diǎn),然后由△MB1Q∽△MON 得對(duì)應(yīng)邊成比例,求出MN、B1Q、MB1的長(zhǎng),再利用三角形的面積公式即可求出點(diǎn)B的坐標(biāo)。
【考點(diǎn)精析】關(guān)于本題考查的反比例函數(shù)的圖象和垂線段最短,需要了解反比例函數(shù)的圖像屬于雙曲線.反比例函數(shù)的圖象既是軸對(duì)稱(chēng)圖形又是中心對(duì)稱(chēng)圖形.有兩條對(duì)稱(chēng)軸:直線y=x和 y=-x.對(duì)稱(chēng)中心是:原點(diǎn);連接直線外一點(diǎn)與直線上各點(diǎn)的所有線段中,垂線段最短;現(xiàn)實(shí)生活中開(kāi)溝引水,牽牛喝水都是“垂線段最短”性質(zhì)的應(yīng)用才能得出正確答案.


 智能訓(xùn)練練測(cè)考系列答案
智能訓(xùn)練練測(cè)考系列答案 計(jì)算高手系列答案
計(jì)算高手系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在平行四邊形ABCD中,過(guò)點(diǎn)A作AE⊥BC,垂足為E,連接DE,F(xiàn)為線段DE上一點(diǎn),且∠AFE=∠B.
(1)求證:△ADF∽△DEC
(2)若AB=4,AD=3 ![]() ,AE=3,求AF的長(zhǎng).
,AE=3,求AF的長(zhǎng).
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】在2016年“雙十一”期間,某快遞公司計(jì)劃租用甲、乙兩種車(chē)輛快遞貨物,從貨物量來(lái)計(jì)算:若租用兩種車(chē)輛合運(yùn),10天可以完成任務(wù);若單獨(dú)租用乙種車(chē)輛,完成任務(wù)的天數(shù)是單獨(dú)租用甲種車(chē)輛完成任務(wù)天數(shù)的2倍.
(1)求甲、乙兩種車(chē)輛單獨(dú)完成任務(wù)分別需要多少天?
(2)已知租用甲、乙兩種車(chē)輛合運(yùn)需租金65000元,甲種車(chē)輛每天的租金比乙種車(chē)輛每天的租金多1500元,試問(wèn):租甲和乙兩種車(chē)輛、單獨(dú)租甲種車(chē)輛、單獨(dú)租乙種車(chē)輛這三種租車(chē)方案中,哪一種租金最少?請(qǐng)說(shuō)明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知:如圖1,OM是∠AOB的平分線,點(diǎn)C在OM上,OC=5,且點(diǎn)C到OA的距離為3.過(guò)點(diǎn)C作CD⊥OA,CE⊥OB,垂足分別為D、E,易得到結(jié)論:OD+OE等于多少;
(1)把圖1中的∠DCE繞點(diǎn)C旋轉(zhuǎn),當(dāng)CD與OA不垂直時(shí)(如圖2),上述結(jié)論是否成立?并說(shuō)明理由;
(2)把圖1中的∠DCE繞點(diǎn)C旋轉(zhuǎn),當(dāng)CD與OA的反向延長(zhǎng)線相交于點(diǎn)D時(shí):
①請(qǐng)?jiān)趫D3中畫(huà)出圖形;
②上述結(jié)論還成立嗎?若成立,請(qǐng)給出證明;若不成立,請(qǐng)直接寫(xiě)出線段OD、OE之間的數(shù)量關(guān)系,不需證明.

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖①,在銳角△ABC中,D,E分別為AB,BC中點(diǎn),F(xiàn)為AC上一點(diǎn),且∠AFE=∠A,DM∥EF交AC于點(diǎn)M.
(1)求證:DM=DA;
(2)如圖②,點(diǎn)G在BE上,且∠BDG=∠C.求證:△DEG∽△ECF;
(3)在(2)的條件下,已知EF=2,CE=3,求GE的長(zhǎng).
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知二次函數(shù)y=a(x﹣h)2+k(a,h,k為常數(shù))在坐標(biāo)平面上的圖象通過(guò)(0,5)、(15,8)兩點(diǎn).若a<0,0<h<10,則h之值可能為下列何值?( )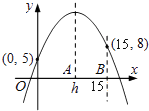
A.5
B.6
C.7
D.8
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
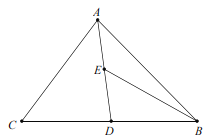
【題目】如圖,![]() 中,
中,![]() 為
為![]() 上一點(diǎn),連接
上一點(diǎn),連接![]() ,
,![]() ,點(diǎn)
,點(diǎn)![]() 在
在![]() 上,連接BE,∠C=∠DEB,若BE=3,AB=4,則線段AE的長(zhǎng)為_____.
上,連接BE,∠C=∠DEB,若BE=3,AB=4,則線段AE的長(zhǎng)為_____.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,PQ為圓O的直徑,點(diǎn)B在線段PQ的延長(zhǎng)線上,OQ=QB=1,動(dòng)點(diǎn)A在圓O的上半圓運(yùn)動(dòng)(含P、Q兩點(diǎn)),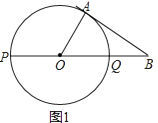
(1)當(dāng)線段AB所在的直線與圓O相切時(shí),求弧AQ的長(zhǎng)(圖1);
(2)若∠AOB=120°,求AB的長(zhǎng)(圖2);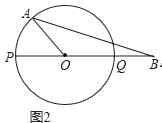
(3)如果線段AB與圓O有兩個(gè)公共點(diǎn)A、M,當(dāng)AO⊥PM于點(diǎn)N時(shí),求tan∠MPQ的值(圖3).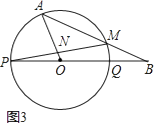
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
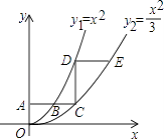
【題目】如圖,平行于x軸的直線AC分別交函數(shù)y1=x2(x≥0)與y2= ![]() (x≥0)的圖象于B、C兩點(diǎn),過(guò)點(diǎn)C作y軸的平行線交y1的圖象于點(diǎn)D,直線DE∥AC,交y2的圖象于點(diǎn)E,則
(x≥0)的圖象于B、C兩點(diǎn),過(guò)點(diǎn)C作y軸的平行線交y1的圖象于點(diǎn)D,直線DE∥AC,交y2的圖象于點(diǎn)E,則 ![]() = .
= . 
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com