
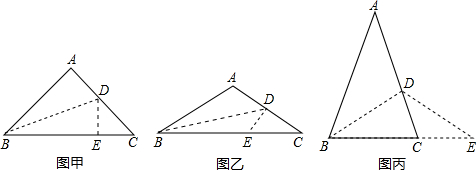
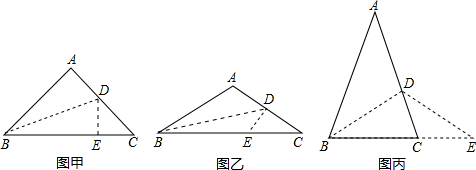
 解:當∠A>90°時(如圖乙),上述結論DE+CD+CE=BC還成立;
解:當∠A>90°時(如圖乙),上述結論DE+CD+CE=BC還成立;

 暑假作業海燕出版社系列答案
暑假作業海燕出版社系列答案 本土教輔贏在暑假高效假期總復習云南科技出版社系列答案
本土教輔贏在暑假高效假期總復習云南科技出版社系列答案 暑假作業北京藝術與科學電子出版社系列答案
暑假作業北京藝術與科學電子出版社系列答案 第三學期贏在暑假系列答案
第三學期贏在暑假系列答案科目:初中數學 來源: 題型:
 (1)化簡:(a-
(1)化簡:(a-| 1 |
| a |
| a2-2a+1 |
| a |
查看答案和解析>>
科目:初中數學 來源: 題型:
 20、如圖,已知,在△ABC中,∠ABC和∠ACB的平分線交于點M,ME∥AB交BC于點E,MF∥AC交BC于點F.求證:△MEF的周長等于BC的長.
20、如圖,已知,在△ABC中,∠ABC和∠ACB的平分線交于點M,ME∥AB交BC于點E,MF∥AC交BC于點F.求證:△MEF的周長等于BC的長.查看答案和解析>>
科目:初中數學 來源: 題型:
 已知:在△ABC中,∠B<∠C,AD平分∠BAC,AE⊥BC,垂足為點E.∠B=38°,∠C=70°.
已知:在△ABC中,∠B<∠C,AD平分∠BAC,AE⊥BC,垂足為點E.∠B=38°,∠C=70°.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com