Question

【題目】已知是⊙的直徑，是⊙的切線，，交⊙于點，是上一點，延長交⊙于點.

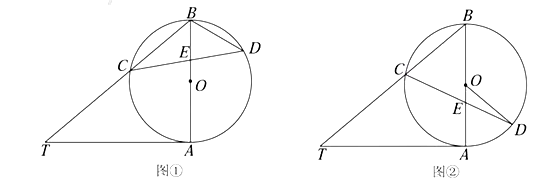
（1）如圖①，求和的大小；

（2）如圖②，當時，求的大小.

Answer 1

【答案】(1) ∠T=40°，∠CDB=40°；（2）∠CDO =15°.

【解析】

試題分析：(1)如圖，連接AC,根據切線的性質定理可得∠TAB=90°，即可求得∠T的度數；根據直徑所對的圓周角為直角可得∠ACB=90°，即可求得∠CDO的度數. （2）如圖，連接AD,在△BCE中，求得∠BCE=∠BEC=65°,根據圓周角定理的推論可得∠BAD=∠BCD=65°，因OA=OD，根據等腰三角形的性質可得∠ODA=∠OAD=65°，即可得∠CDO=∠ODA-∠ADC=15°.

試題解析：(1)如圖，連接AC,

∵是⊙的直徑，是⊙的切線，

∴AT⊥AB,即∠TAB=90°.

∵，

∴∠T=90°-∠ABT=40°

由是⊙的直徑，得∠ACB=90°，

∴∠CAB=90°-∠ABC=40°

∴∠CDB=∠CAB=40°;

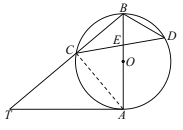
（2）如圖，連接AD,

在△BCE中，BE=BC，∠EBC=50°，

∴∠BCE=∠BEC=65°,

∴∠BAD=∠BCD=65°

∵OA=OD

∴∠ODA=∠OAD=65°

∵∠ADC=∠ABC=50°

∴∠CDO=∠ODA-∠ADC=15°.