
【題目】閱讀理解:若在一個兩位正整數N的個位數字與十位數字之間添上數字6,組成一個新的三位數,我們稱這個三位數為N的“至善數”,如34的“至善數為364”;若將一個兩位正整數M加6后得到一個新數,我們稱這個新數為M的“明德數”,如34的“明德數為40”.
(1)30的“至善數”是 ,“明德數”是 .
(2)求證:對任意一個兩位正整數A,其“至善數”與“明德數”之差能被9整除;
(3)若一個兩位正整數B的明德數的各位數字之和是B的至善數各位數字之和的一半,求B的最大值.
【答案】(1)360;36;(2)答案見解析;(3)84.
【解析】
(1)根據“至善數”和“明德數”的定義計算即可得答案;(2)設A的十位數字為a,個位數字為b,分別寫出A的“至善數”和“明德數”,求差,化簡,表示出9的倍數,即可證明;(3)設B的十位數字為a,個位數字為b,分別寫出B的“至善數”和“明德數”的各個數位上的數字之和,“明德數”的個位可能存在進位,故分兩類計算即可.
解:(1)在3和0之間添上數字6,
∴30的“至善數是360;“明德數“是30+6=36
故答案為:360;36.
(2)證明:設A的十位數字為a,個位數字為b
則其“至善數與“明德數“分別為:
100a+60+b;10a+b+6
它們的差為:
100a+60+b-(10a+b+6)
=90a+54
=9(10a+6)
∴其“至善數與“明德數“之差能被9整除.
(3)設B的十位數字為a,個位數字為b
則B的至善數的各位數字之和是a+6+b
B的明德數各位數字之和是a+b+6(當0≤b<4時)或a+1+(6+b-10)(當4≤b≤9時)
由題意得:0≤b<4時,a+b+6=![]() (a+6+b)
(a+6+b)
∴a+b=-6,不符合題意;
當4≤b≤9時,a+1+(6+b-10)=![]() (a+6+b)
(a+6+b)
∴a+b=12
∴當b=4,a=8時,B最大,最大值為84.


科目:初中數學 來源: 題型:
【題目】某游泳池有900立方米水,每次換水前后水的體積保持不變.設放水的平均速度為v立方米/小時,將池內的水放完需t小時,
(1)求v關于t的函數表達式,并寫出自變量t的取值范圍;
(2)若要求在2.5小時至3小時內(包括2.5小時與3小時)把游泳池內的水放完,求放水速度的范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
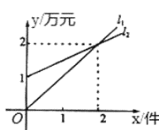
【題目】如圖,![]() 表示某機床公司一天的銷售收入與機床銷售量的關系,
表示某機床公司一天的銷售收入與機床銷售量的關系,![]() 表示該公司一天的銷售成本與機床銷售量的關系.有以下四個結論:①
表示該公司一天的銷售成本與機床銷售量的關系.有以下四個結論:①![]() 對應的函數表達式是y=x;②
對應的函數表達式是y=x;②![]() 對應的函數表達式是y=x+1;③當銷售量為2件時,銷售收入等于銷售成本;④利潤與銷售量之間的函數表達式是w=0.5x-1.其中正確的結論為____(請把所有正確的序號填寫在橫線上).
對應的函數表達式是y=x+1;③當銷售量為2件時,銷售收入等于銷售成本;④利潤與銷售量之間的函數表達式是w=0.5x-1.其中正確的結論為____(請把所有正確的序號填寫在橫線上).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校為表彰在“創文明城,點贊泰城”書畫比賽中表現優秀的同學,決定購買水彩盒或鋼筆作為獎品。已知1個水彩盒28元、1支鋼筆30元。
(1)恰逢“十一”商店舉行“優惠促銷”活動,具體辦法如下:水彩盒“九折”優惠;鋼筆10支以上超出部分“八折”優惠。若買![]() 個水彩盒需要
個水彩盒需要![]() 元,買
元,買![]() 支鋼筆需要
支鋼筆需要![]() 元,求
元,求![]() ,
,![]() 關于
關于![]() 的函數關系式.
的函數關系式.
(2)當購買數量為多少時,購買兩種獎品的費用相同?
(3)當購買數量為80時,購買兩種獎品的費用差距是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀理解:若 ![]() 為數軸上三點,若點
為數軸上三點,若點![]() 到
到![]() 的距離是點
的距離是點![]() 到
到![]() 的距離
的距離![]() 倍,我們就稱點
倍,我們就稱點![]() 是
是![]() 的巧點.若
的巧點.若 ![]() 為數軸上三點,若點
為數軸上三點,若點![]() 到
到![]() 的距離是點
的距離是點![]() 到
到 ![]() 的距離一半,我們就稱點
的距離一半,我們就稱點![]() 是
是![]() 的妙點.如圖,點
的妙點.如圖,點![]() 表示的數為
表示的數為![]() ,點
,點![]() 表示的數為
表示的數為![]() ,表示
,表示![]() 的點
的點![]() 到點
到點![]() 的距離是
的距離是![]() ,到點
,到點![]() 的距離是
的距離是![]() ,那么點
,那么點![]() 是
是![]() 的巧點,點
的巧點,點![]() 是
是![]() 的妙點.
的妙點.
![]()
知識運用:
(1)如圖 1,點![]() 表示的數是
表示的數是![]() ,點
,點![]() 表示的數是
表示的數是![]() ,點
,點![]() 表示的數是
表示的數是![]() ,那么點
,那么點![]() 是(
是(![]() 的( )
的( )
![]()
A.巧點 B. 妙點 C. 無法確定
(2)如圖 2,![]() 為數軸上兩點,點
為數軸上兩點,點![]() 所表示的數為
所表示的數為![]() ,點
,點![]() 所表示的數為
所表示的數為![]() ,則(
,則(![]() 的巧點表示的數是 ;
的巧點表示的數是 ;
![]()

拓展提升
(3)如圖 3,![]() 為數軸上兩點,點
為數軸上兩點,點![]() 所表示的數為
所表示的數為![]() ,點
,點![]() 所表示的數為
所表示的數為![]() .現有一只電子螞蟻P從點
.現有一只電子螞蟻P從點 ![]() 出發,以每
出發,以每![]() 秒單位的速度向右運動,到達點
秒單位的速度向右運動,到達點![]() 停止. 當經過幾秒時,
停止. 當經過幾秒時,![]() 和
和 ![]() 其有一個點為其余兩點的巧點? (請直接寫出結果)
其有一個點為其余兩點的巧點? (請直接寫出結果)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點![]() 都在數軸上,
都在數軸上,![]() 為原點.
為原點.
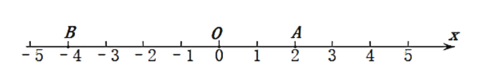
(1)線段![]() 中點表示的數是 ;
中點表示的數是 ;
(2)若點![]() 以每秒
以每秒![]() 個單位長度的速度沿數軸向右運動了
個單位長度的速度沿數軸向右運動了![]() 秒,當點
秒,當點![]() 在點
在點![]() 左邊時,
左邊時,![]() ,當點
,當點![]() 至點
至點![]() 右邊時,
右邊時,![]() ;
;
(3)若點![]() 分別以每秒
分別以每秒![]() 個單位長度、
個單位長度、![]() 個單位長度的速度沿數軸向右運動,而點
個單位長度的速度沿數軸向右運動,而點![]() 不動,
不動,![]() 秒后,
秒后,![]() 三個點中有一個點是另外兩個點為端點的線段的中點,求
三個點中有一個點是另外兩個點為端點的線段的中點,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某市需調查該市九年級男生的體能狀況,為此抽取了50名九年級男生進行引體向上個數測試,測試情況繪制成表格如下:
個數 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
人數 | 1 | 1 | 6 | 18 | 10 | 6 | 2 | 2 | 1 | 1 | 2 |
(1)求這次抽樣測試數據的平均數、眾數和中位數;
(2)在平均數、眾數和中位數中,你認為用哪一個統計量作為該市九年級男生引體向上項目測試的合格標準個數較為合適?簡要說明理由;
(3)如果該市今年有3萬名九年級男生,根據(2)中你認為合格的標準,試估計該市九年級男生引體向上項目測試的合格人數是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(8分)如圖,點A(3,5)關于原點O的對稱點為點C,分別過點A,C作y軸的平行線,與反比例函數![]() (0<k<15)的圖象交于點B,D,連接AD,BC,AD與x軸交于點E(﹣2,0).
(0<k<15)的圖象交于點B,D,連接AD,BC,AD與x軸交于點E(﹣2,0).

(1)求k的值;
(2)直接寫出陰影部分面積之和.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲、乙兩人各射擊![]() 次,甲所中的環數是
次,甲所中的環數是![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,且甲所中的環數的平均數是
,且甲所中的環數的平均數是![]() ,眾數是
,眾數是![]() ;乙所中的環數的平均數是
;乙所中的環數的平均數是![]() ,方差是4.根據以上數據,對甲,乙射擊成績的正確判斷是( )
,方差是4.根據以上數據,對甲,乙射擊成績的正確判斷是( )
A.甲射擊成績比乙穩定B.乙射擊成績比甲穩定
C.甲,乙射擊成績穩定性相同D.甲、乙射擊成績穩定性無法比較
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com