【題目】如圖，
是
的直徑，弦
于點
，
是
上一點，
，
的延長線交于點
，連接
，
，
．
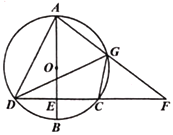
（1）求證：
．
（2）已知
，
．
①求的半徑長．
②若點是
的中點，求
與
的面積之比．
【答案】(1)詳見解析;(2)①5;②
【解析】
（1）連接
，根據直徑所對的圓周角是直角可得
，從而得出
，然后根據直角三角形的兩個銳角互余可得
，從而得出
，即可證出結論；
（2）①根據垂徑定理和條件可得
，連接
，設
的半徑為
，根據勾股定理列出方程即可求出結論；
②由①結論求出AE、DE，根據勾股定理求出AD，根據相似三角形的判定定理可得
，列出比例式即可求出AG和AF，然后利用勾股定理求出EF，即可求出FD，根據三角形中線的性質可得
，最后根據等高的兩個三角形面積比等于底之比即可求出結論．
（1）證明：連接
∵
是的直徑
∴
∴
∵
∴
∴
∵
∴
（2）①∵，
∴
連接，設的半徑為
則
，
，
∴
解得
即的半徑長為5．
②∵
，
∴
∵，
∴
∴
∵點
是
的中點
∴
∴
，
∴
∴
∴點是的中點
∴
∴
科目：初中數學 來源： 題型：
【題目】記某商品銷售單價為x元，商家銷售此種商品每月獲得的銷售利潤為y元，且y是關于x的二次函數．已知當商家將此種商品銷售單價分別定為55元或75元時，他每月均可獲得銷售利潤1800元；當商家將此種商品銷售單價定為80元時，他每月可獲得銷售利潤1550元，則y與x的函數關系式是（ ）
A.y＝﹣（x﹣60）2+1825B.y＝﹣2（x﹣60）2+1850
C.y＝﹣（x﹣65）2+1900D.y＝﹣2（x﹣65）2+2000
查看答案和解析>>
科目：初中數學 來源： 題型：
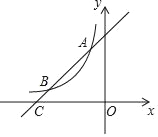
【題目】如圖，一次函數y=x+4的圖象與反比例函數y=
（k為常數且k≠0）的圖象交于A（﹣1，a），B兩點，與x軸交于點C．
（1）求此反比例函數的表達式；
（2）若點P在x軸上，且S△ACP=
S△BOC，求點P的坐標．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某商店購進
、
兩種商品，購買1個商品比購買1個商品多花10元，并且花費300元購買商品和花費100元購買商品的數量相等．
（1）求購買一個商品和一個商品各需要多少元；
（2）商店準備購買、兩種商品共80個，若商品的數量不少于商品數量的4倍，并且購買、商品的總費用不低于1000元且不高于1050元，那么商店有哪幾種購買方案？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在△ABC中，AB＝AC，CD是AB邊上的中線，點E在邊AC上（不與A，C重合），且BE＝CD．設
＝k，若符合條件的點E有兩個，則k的取值范圍是_____．
查看答案和解析>>
科目：初中數學 來源： 題型：
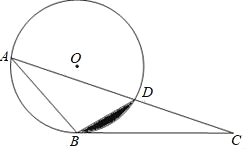
【題目】如圖，△ABC中，⊙O經過A、B兩點，且交AC于點D，連接BD，∠DBC＝∠BAC．
（1）證明BC與⊙O相切；
（2）若⊙O的半徑為6，∠BAC＝30°，求圖中陰影部分的面積．
查看答案和解析>>
科目：初中數學 來源： 題型：
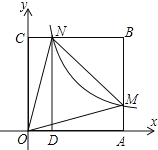
【題目】如圖，在平面直角坐標系中，正方形OABC的頂點O與原點重合，頂點A，C分別在x軸、y軸上，反比例函數
(k≠0，x>0)的圖象與正方形的兩邊AB、BC分別交于點M、N，連接OM、ON、MN．若∠MON=45°，MN=2，則k的值為_______．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖1，在菱形
中，動點P從點B出發，沿折線B→C→D→B運動，設點P經過的路程為x，
的面積為y.把y看作x的函數，函數的圖象如圖2所示，則圖2中的a等于（ ）
A.25B.20C.12D.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
