
【題目】把兩個全等的等腰直角三角板(直角邊長為4)疊放在一起,且三角板EFG的直角頂點G位于三角板ABC的斜邊中點處.現將三角板EFG繞G點按順時針方向旋轉α度(0°<α<90°)(如圖1),四邊形GKCH為兩三角板的重疊部分.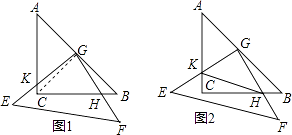
(1)猜想BH與CK有怎樣的數量關系?并證明你的結論;
(2)連接HK(如圖2),在上述旋轉過程中,設BH=x,△GKH的面積為y,
①求y與x之間的函數關系式,并寫出自變量x的取值范圍;
②當△GKH的面積恰好等于△ABC面積的 ![]() ,求x.
,求x.
【答案】
(1)
解:BH=CK.
理由如下:∵點O是等腰直角三角板ABC斜邊中點,
∴∠B=∠GCK=45°,BG=CG,
由旋轉的性質,知∠BGH=∠CGK,
在△BGH和△CGK中,
 ,
,
∴△BGH≌△CGK(ASA),
∴BH=CK;
(2)
解:①∵△BGH≌△CGK,
∴S四邊形CHGK=S△CGK+S△CGH=S△BGH+S△CGH=S△BCG= ![]() S△ABC=4,
S△ABC=4,
∴S△GKH=S四邊形CHGK﹣S△KCH=4﹣ ![]() CH×CK,
CH×CK,
∴y= ![]() x2﹣2x+4(0<x<4),
x2﹣2x+4(0<x<4),
②當y= ![]() ×8=
×8= ![]() 時,即
時,即 ![]() x2﹣2x+4=
x2﹣2x+4= ![]() ,
,
∴x=1 或x=3.
∴當△GKH的面積恰好等于△ABC面積的 ![]() 時,BH=1 或BH=3.
時,BH=1 或BH=3.
【解析】(1)先由ASA證出△CGK≌△BGH,再根據全等三角形的性質得出BH=CK,根據全等得出四邊形CKGH的面積等于三角形ACB面積一半;(2)①由(1)易得S四邊形CHGK= ![]() S△ABC , 然后根據面積公式得出y=
S△ABC , 然后根據面積公式得出y= ![]() x2﹣2x+4;②根據△GKH的面積恰好等于△ABC面積的
x2﹣2x+4;②根據△GKH的面積恰好等于△ABC面積的 ![]() ,代入得出方程即可求得結果.
,代入得出方程即可求得結果.


科目:初中數學 來源: 題型:
【題目】問題背景:
如圖1,在四邊形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,EF分別是BC,CD上的點,且∠EAF=60°,探究圖中線段BE,EF,FD之間的數量關系.
小王同學探究此問題的方法是延長FD到點G,使DG=BE,連結AG,先證明△ABE≌△ADG,再證明△AEF≌△AGF,可得出結論,他的結論應是__________________;
探索延伸:
如圖2,若在四邊形ABCD中,AB=AD,∠B+∠D=180°,E,F分別是BC,CD上的點,且∠EAF=![]() ∠BAD,上述結論是否仍然成立,并說明理由;
∠BAD,上述結論是否仍然成立,并說明理由;
結論應用:
如圖3,在某次軍事演習中,艦艇甲在指揮中心(O處)北偏西30°的A處,艦艇乙在指揮中心南偏東70°的B處,并且兩艦艇到指揮中心的距離相等.接到行動指令后,艦艇甲向正東方向以50海里/小時的速度前進,艦艇乙沿北偏東50°的方向以60海里/小時的速度前進,1.5小時后,指揮中心觀測到甲、乙兩艦艇分別到達E,F處,且兩艦艇與指揮中心O之間夾角∠EOF=70°,試求此時兩艦艇之間的距離.
能力提高:
如圖4,等腰直角三角形ABC中,∠BAC=90°,AB=AC,點M,N在邊BC上,且∠MAN=45°.若BM=5,CN=12,則MN的長為_________.(直接寫出答案)




查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某中學為了綠化校園,計劃購買一批榕樹和香樟樹,經市場調查,榕樹的單價比香樟樹少20元,購買3棵榕樹和2棵香樟樹共需340元.
(1)榕樹和香樟樹的單價各是多少?
(2)根據學校實際情況,需購買兩種樹苗共150棵,總費用不超過10840元,且購買香樟樹的棵數不少于榕樹的1.5倍,請你算算該校本次購買榕樹和香樟樹共有哪幾種方案.
查看答案和解析>>
科目:初中數學 來源: 題型:
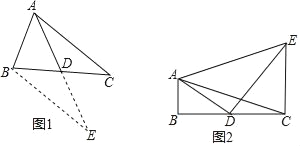
【題目】數學興趣小組在活動時,老師提出了這樣一個問題:如圖1,在△ABC中,AB=8,AC=6,D是BC的中點,求BC邊上的中線AD的取值范圍.
小明在組內經過合作交流,得到了如下的解決方法:延長AD到E,使DE=AD,再證明“△ADC≌△EDB”.
(1)探究得出AD的取值范圍是_____;
(2)(問題解決)如圖2,△ABC中,∠B=90°,AB=2,AD是△ABC的中線,CE⊥BC,CE=4,且∠ADE=90°,求AE的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在5×4正方形網格中,有A,B,C三個格點(線與線的交點).
(1)若小正方形邊長為1,則AC= , AB=;
(2)在圖中再找出一個格點D,滿足:D與A,B,C三點中的兩點組成的三角形恰好與△ABC相似:∽△ABC.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,在等腰直角△ABC中,∠B=90°,將△ABC繞點 A逆時針旋轉60°后得到的△AB′C′,則∠BAC′等于( ) 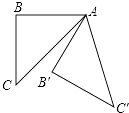
A.105°
B.120°
C.135°
D.150°
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知二次函數y=﹣x2+2x+m.
(1)如果二次函數的圖象與x軸有兩個交點,求m的取值范圍;
(2)如圖,二次函數的圖象過點A(3,0),與y軸交于點B,直線AB與這個二次函數圖象的對稱軸交于點P,求點P的坐標. 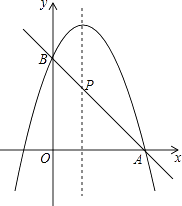
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】飛機著陸后滑行的距離S(單位:m)關于滑行時間t(單位:s)的函數解析式是:S=60t﹣1.5t2
(1)直接指出飛機著陸時的速度;
(2)直接指出t的取值范圍;
(3)畫出函數S的圖象并指出飛機著陸后滑行多遠才能停下來? 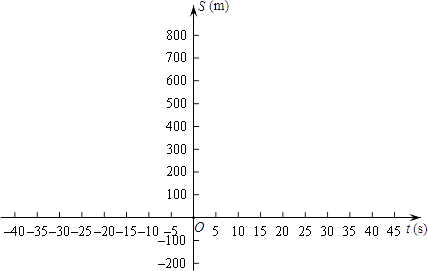
查看答案和解析>>
科目:初中數學 來源: 題型:
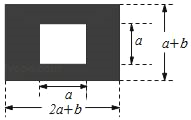
【題目】如圖,某市有一塊長為(2a+b)米,寬為(a+b)米的長方形地塊,規劃部門計劃將陰影部分進行綠化,中間將修建一座雕像.
(1)試用含a,b的代數式表示綠化的面積是多少平方米?
(2)若a=3,b=2,請求出綠化面積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com