【題目】下表為某班學生成績的次數(shù)分配表．已知全班共有
人，且眾數(shù)為
分，中位數(shù)為
分，則
之值為________．
成績 （分） |
|
|
|
|
|
|
|
|
次數(shù) （人） |
|
|
|
|
|
|
|
|
【答案】57
【解析】
由于全班共有38人，則x+y=38-（2+3+5+6+3+4）=15，結合眾數(shù)為50分，中位數(shù)為60分，分情況討論即可確定x、y之值，從而求出x2-y之值．
∵全班共有38人，
∴x+y=38-（2+3+5+6+3+4）=15，
又∵眾數(shù)為50分，
∴x>6，x>y，
∴x≥8，
當x=8時，y=7，中位數(shù)是第19、20兩個數(shù)的平均數(shù)，都為60分，則中位數(shù)為60分，符合題意；
當x=9時，y=6，中位數(shù)是第19、20兩個數(shù)的平均數(shù)，則中位數(shù)為（50+60）÷2=55分，不符合題意；
同理當x=10，11，12，13，14，15時，中位數(shù)都不等于60分，不符合題意．
∴x=8，y=7．
∴x2-y=64-7=57．
故答案為：57．
科目：初中數(shù)學 來源： 題型：
【題目】如圖(1)，在
中，
，
，
，若動點P從點A開始沿著
的路徑運動，且速度為每秒2cm，設點P運動的時間為t秒.
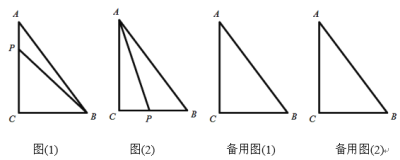
(1)當
時，
的面積是___________
；
(2)如圖(2)當t為何值時，AP平分
；
(3)當t為何值時，
為等腰三角形.
查看答案和解析>>
科目：初中數(shù)學 來源： 題型：
【題目】若二次函數(shù)
的圖象與
軸的交點坐標分別為
，
，且
，圖象上有一點
在軸下方，對于以下說法：
①
；②
是方程
的解；③
；
④
．其中正確的是________．
查看答案和解析>>
科目：初中數(shù)學 來源： 題型：
【題目】如圖，點E, F在直線AC上，DF=BE， ∠AFD=∠CEB,下列條件中不能判斷△ADF≌△CBE的是( )
A.∠D=∠BB.AD=CBC.AE=CFD.AD// BC
查看答案和解析>>
科目：初中數(shù)學 來源： 題型：
【題目】某商場銷售一批名牌襯衫，平均每天可售出
件，每件盈利
元，為擴大銷售增加盈利，盡快減少庫存，商場決定采取適當?shù)慕祪r措施，經調查發(fā)現(xiàn)，如果每件襯衫每降價一元，市場每天可多售
件，問他降價多少元時，才能使每天所賺的利潤最大？并求出最大利潤．
查看答案和解析>>
科目：初中數(shù)學 來源： 題型：
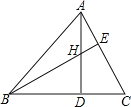
【題目】如圖，在△ABC中，高AD和BE交于點H，∠ABC=45°，BE平分∠ABC,下列結論:①∠DAC= 22.5°；②BH= 2CE； ③若連結CH,則CH⊥AB；④若CD=1,則AH=2；其中正確的有( )
A.1個
B.2個
C.3個
D.4個
查看答案和解析>>
科目：初中數(shù)學 來源： 題型：
【題目】如圖，網格中每個小正方形的邊長為1,點B、C的坐標分別為(-1, 3), (0, 1).
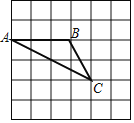
(1)建立符合條件的直角坐標系(要求標出x軸，y軸和原點)，并寫出點A的坐標
(2)線段AB上任意一點的坐標可以表示為
(3)在y軸上找到一點P,使得S△ABP = 3S△ABC，求出點P的坐標.
查看答案和解析>>
科目：初中數(shù)學 來源： 題型：
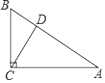
【題目】如圖，在△ABC中，∠ACB＝90°，過點C作CD⊥AB于D，∠A＝30°，BD＝1，則AB的值是（ ）.
A.1B.2C.3D.4
查看答案和解析>>
科目：初中數(shù)學 來源： 題型：
【題目】閱讀、思考、解決問題：
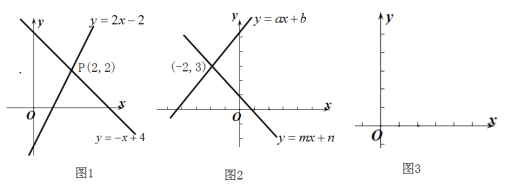
（1）如圖（1）兩個函數(shù)
和
的圖象交于點
，的坐標
是否滿足這兩個函數(shù)式？即
是方程的解嗎？是方程的解嗎？答： ① （是、不是）這就是說：函數(shù)和圖象的交點坐標 ② （是、不是）方程組
的解；反之，方程組的解 ③ （是、不是）函數(shù)和圖象的交點坐標．
（2）根據(jù)圖（2）寫出方程組
的解是：____________
（3）已知兩個一次函數(shù)
和
．
①求這兩個函數(shù)圖象的交點坐標；
②在圖（3）的坐標系中畫出這兩個函數(shù)的圖象
③根據(jù)圖象寫出當
時，
的取值范圍．
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
