
已知:如圖,等邊三角形ABC內接于⊙O,點P是劣弧![]() 上的一點(端點除外),延長BP至D,使BD=AP,連接CD。
上的一點(端點除外),延長BP至D,使BD=AP,連接CD。

(1)若AP過圓心O,如圖(1),請你判斷△PDC是什么三角形,并說明理由。
(2)若AP不過圓心O,如圖(2),△PDC又是什么三角形?為什么?
解:(1)△PDC為等邊三解形
理由:∵△ABC為等邊三角形,∴AC=BC
在⊙O中,∠PAC=∠DBC,又∵AP=BD,∴△APC≌△BDC
∴PC=DC 又∵AP過圓心O,AB=AC,∠BAC=60°,
∴∠BAP=∠PAC=![]() ∠BAC=30°
∠BAC=30°
∴∠BAP=∠BCP=30°,∠PBC=∠PAC=30°
∴∠CPD=∠PBC+∠BCP=30°+30°=60°
∴△PDC為等邊三角形
(2)△PDC仍為等邊三角形
理由:先證△APC≌△BDC (過程同上)。
∴PC=DC
∴∠BAP+∠PAC=60°,
又∵∠BAP=∠BCP,∠PAC=∠PBC,
∴∠CPD=∠BCP+∠PBC=∠BAP+∠PAC=60°
又∵PC=DC,∴△PDC為等邊三角形。


科目:初中數(shù)學 來源: 題型:
 類似地你可以得到:“滿足
類似地你可以得到:“滿足查看答案和解析>>
科目:初中數(shù)學 來源: 題型:

查看答案和解析>>
科目:初中數(shù)學 來源:2010年高級中等學校招生全國統(tǒng)一考試數(shù)學卷(江蘇南京) 題型:解答題
學習《圖形的相似》后,我們可以探索兩個直角三角形全等的條件所獲得的經驗,繼續(xù)探索兩個直角三角形相似的條件.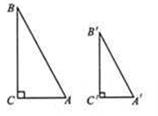
(1)“對于兩個直角三角形,滿足一邊一銳角對應相等,或兩直角邊對應相等,兩個直角三角形全等”,類似地,你可以得到“滿足_____,或_____,兩個直角三角形相似”;
(2)“滿足斜邊和一條直角邊對應相等的兩個直角三角形全等”,類似地,你可以得到滿足_____兩個直角三角形相似”.請結合下列所給圖形,寫出已知,并完成說理過程.
已知:如圖,_____.試說明Rt△ABC∽Rt△A/B/C/.
查看答案和解析>>
科目:初中數(shù)學 來源:2010-2011學年北京市考數(shù)學一模試卷 題型:選擇題
已知:如圖,在等邊三角形ABC中,M、N分別是AB、AC的中點,D是MN上任意一點,CD、BD的延長線分別與AB、AC交于F、E,若 ,則等邊三角
,則等邊三角
形ABC的邊長為

A. 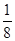 B.
B.  C.
C.
 D.1
D.1
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
已知:如圖,在等邊三角形ABC中,M、N分別是AB、AC的中點,D是MN上任意一點,CD、BD的延長線分別與AB、AC交于F、E,若![]() ,則等邊三角
,則等邊三角
形ABC的邊長為
A. ![]() B.
B. ![]() C.
C.![]() D.1
D.1
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com