
【題目】如圖,在矩形ABCD中,AB=![]() ,AD=10.連接BD,∠DBC的角平分線BE交DC于點E,現把△BCE繞點B逆時針旋轉,記旋轉后的△BCE為△BC′E′.當射線BE′和射線BC′都與線段AD相交時,設交點分別為F,G.若△BFD為等腰三角形,則線段DG長為 .
,AD=10.連接BD,∠DBC的角平分線BE交DC于點E,現把△BCE繞點B逆時針旋轉,記旋轉后的△BCE為△BC′E′.當射線BE′和射線BC′都與線段AD相交時,設交點分別為F,G.若△BFD為等腰三角形,則線段DG長為 .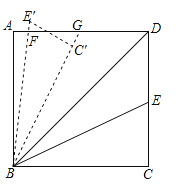
【答案】![]()
【解析】解:過E作EO⊥BD于O,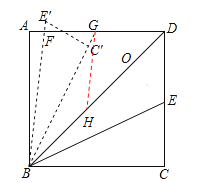
在Rt△ABD中,由勾股定理,得
BD=![]() =
=![]() =14,
=14,
在Rt△ABF中,由勾股定理,得:
BF2=(4![]() )2+(10﹣BF)2 ,
)2+(10﹣BF)2 ,
解得BF=![]() ,
,
AF=10﹣![]() =
=![]() .
.
過G作GH∥BF,交BD于H,
∴∠FBD=∠GHD,∠BGH=∠FBG,
∵FB=FD,
∴∠FBD=∠FDB,
∴∠FDB=∠GHD,
∴GH=GD,
∵∠FBG=∠EBC=![]() ∠DBC=
∠DBC=![]() ∠ADB=
∠ADB=![]() ∠FBD,
∠FBD,
又∵∠FBG=∠BGH,∠FBG=∠GBJ,
∴BH=GH,
設DG=GH=BH=x,則FG=FD﹣GD=![]() ﹣x,HD=14﹣x,
﹣x,HD=14﹣x,
∵GH∥FB,
∴![]() ,即
,即![]() ,
,
解得x=![]() .
.
所以答案是:![]() .
.
【考點精析】通過靈活運用旋轉的性質,掌握①旋轉后對應的線段長短不變,旋轉角度大小不變;②旋轉后對應的點到旋轉到旋轉中心的距離不變;③旋轉后物體或圖形不變,只是位置變了即可以解答此題.


科目:初中數學 來源: 題型:
【題目】如圖,在直角坐標系中,⊙A的圓心A的坐標為(﹣1,0),半徑為1,點P為直線y=﹣ ![]() x+3上的動點,過點P作⊙A的切線,切點為Q,則切線長PQ的最小值是 .
x+3上的動點,過點P作⊙A的切線,切點為Q,則切線長PQ的最小值是 . 
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小明在學習了正方形之后,給同桌小文出了道題,從下列四個條件:①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD中選兩個作為補充條件,使ABCD為正方形(如圖),現有下列四種選法,你認為其中錯誤的是( )
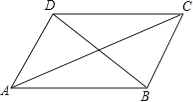
A.①②B.②③C.①③D.②④
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在正方形ABCD中,AD=2 ![]() ,把邊BC繞點B逆時針旋轉30°得到線段BP,連接AP并延長交CD于點E,連接PC,則三角形PCE的面積為 .
,把邊BC繞點B逆時針旋轉30°得到線段BP,連接AP并延長交CD于點E,連接PC,則三角形PCE的面積為 . 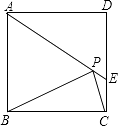
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在菱形ABCD中,AB=2,∠BAD=60°,過點D作DE⊥AB于點E,DF⊥BC于點F.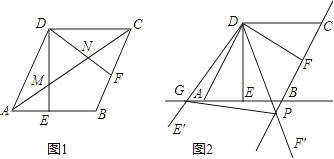
(1)如圖1,連接AC分別交DE、DF于點M、N,求證:MN= ![]() AC;
AC;
(2)如圖2,將△EDF以點D為旋轉中心旋轉,其兩邊DE′、DF′分別與直線AB、BC相交于點G、P,連接GP,當△DGP的面積等于3 ![]() 時,求旋轉角的大小并指明旋轉方向.
時,求旋轉角的大小并指明旋轉方向.
查看答案和解析>>
科目:初中數學 來源: 題型:
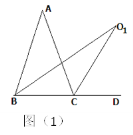
【題目】如圖 ⑴![]() 的平分線和外角
的平分線和外角![]() 的平分線相交于
的平分線相交于![]() 點,
點,![]() 。
。
(1)求![]() 的度數;(寫理由)
的度數;(寫理由)
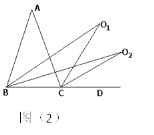
(2)如圖(2),在⑴的條件下,再畫![]() 和
和![]() 的角平分線相交于
的角平分線相交于![]() 點,求
點,求![]() 的度數;
的度數;
(3)若![]() ,按上述規律繼續畫下去,請直接寫出
,按上述規律繼續畫下去,請直接寫出![]() 的度數。
的度數。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com