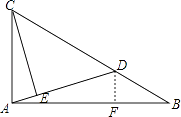
【題目】如圖，已知點D是Rt△ABC的斜邊BC上的一點，tanB= 
，BC=3BD，CE⊥AD，則 
= ． 
【答案】
【解析】解：過點D作DF⊥AB于點F， ∵∠CAB=90°，DF⊥AB，
∴AC∥DF，
∴ 
=
∵BC=3BD，
∴ = 
，
∴AF=kBF
∵tanB= ，
∴ 
= ，
∴DF= FB，
∴ 
，
∵CE⊥AD，
∴tan∠ACE= 
，
∵∠CAE+∠ACE=90°，∠CAE+∠DAB=90°，
∴∠ACE=∠DAF，
∴tan∠ACE=tan∠DAF= 
．
所以答案是： ．
【考點精析】本題主要考查了勾股定理的概念和相似三角形的判定與性質的相關知識點，需要掌握直角三角形兩直角邊a、b的平方和等于斜邊c的平方,即;a2+b2=c2；相似三角形的一切對應線段(對應高、對應中線、對應角平分線、外接圓半徑、內切圓半徑等）的比等于相似比；相似三角形周長的比等于相似比；相似三角形面積的比等于相似比的平方才能正確解答此題．
科目：初中數學 來源： 題型：
【題目】如圖，在△ABC中，∠ACB＝90°，分別以點A和點B為圓心，以相同的長（大于
AB）為半徑作弧，兩弧相交于點M和點N，作直線MN交AB于點D，交BC于點E．若AC＝3，AB＝5，則DE等于（ ）
A. 2 B. 
C. 
D. 
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知代數式A＝x2＋3xy＋x－
，B＝2x2－xy＋4y－1
（1）當x＝y＝－2時，求2A－B的值；
（2）若2A－B的值與y的取值無關，求x的值．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】【問題情境】
如圖1，四邊形ABCD是正方形，M是BC邊上的一點，E是CD邊的中點，AE平分∠DAM．
【探究展示】
（1）證明：AM=AD+MC；
（2）AM=DE+BM是否成立？若成立，請給出證明；若不成立，請說明理由．
【拓展延伸】
（3）若四邊形ABCD是長與寬不相等的矩形，其他條件不變，如圖2，探究展示（1）、（2）中的結論是否成立？請分別作出判斷，不需要證明．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，正方形ABCD中，AB=1，點P是BC邊上的任意一點（異于端點B、C），連接AP，過B、D兩點作BE⊥AP于點E，DF⊥AP于點F.
（1）求證：EF=DF﹣BE；
（2）若△ADF的周長為
，求EF的長.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】（概念學習）
規定：求若干個相同的有理數（均不等于0）的除法運算叫做除方，如2÷2÷2等．類比有理數的乘方，我們把2÷2÷2記作2③，讀作“2的圈3次方”，一般地，把
（a≠0）記作a，讀作“a的圈n次方”．
（初步探究）
(1)直接寫出計算結果：2③=_____，（﹣
）⑤=_____．
(2)關于除方，下列說法準確的選項有_________（只需填入正確的序號）
①.任何非零數的圈2次方都等于1； ②．對于任何正整數n，1=1；
③.3④=4③ ④．負數的圈奇數次方結果是負數，負數的圈偶數次方結果是正數．
（深入思考）我們知道，有理數的減法運算可以轉化為加法運算，除法運算可以轉化為乘法運算，有理數的除方運算如何轉化為乘方運算呢？
例如： 2④=2÷2÷2÷2
=2×××
=（__）2 (冪的形式)
試一試：將下列除方運算直接寫成冪的形式．
5⑥=_____；(﹣)⑩=_____；a=_____（a≠0）．
算一算：
④÷23+（﹣8）×2③．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，AC是⊙O的直徑，BC是⊙O的弦，點P是⊙O外一點，連接PB、AB，∠PBA=∠C．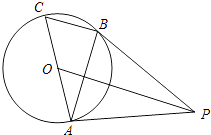 
（1）求證：PB是⊙O的切線；
（2）連接OP，若OP∥BC，且OP=8，⊙O的半徑為2 
，求BC的長．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，函數y= 
的圖象過點A（1，2）．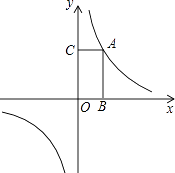 
（1）求該函數的解析式；
（2）過點A分別向x軸和y軸作垂線，垂足為B和C，求四邊形ABOC的面積；
（3）求證：過此函數圖象上任意一點分別向x軸和y軸作垂線，這兩條垂線與兩坐標軸所圍成矩形的面積為定值．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com