
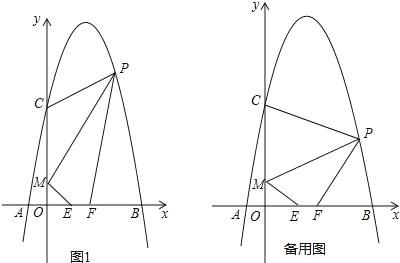
【題目】如圖,對稱軸為直線x=2的拋物線經過A(﹣1,0),C(0,5)兩點,與x軸另一交點為B.已知M(0,1),E(a,0),F(a+1,0),點P是第一象限內的拋物線上的動點.
(1)求此拋物線的解析式;
(2)當a=1時,求四邊形MEFP的面積的最大值,并求此時點P的坐標;
(3)若△PCM是以點P為頂點的等腰三角形,求a為何值時,四邊形PMEF周長最小?請說明理由.
【答案】(1)y=﹣(x﹣2)2+9=﹣x2+4x+5;
(2)當x=![]() 時,四邊形MEFP的面積有最大值為
時,四邊形MEFP的面積有最大值為![]() ,點P坐標為(
,點P坐標為(![]() ,
,![]() );
);
(3)a=![]() 時,四邊形PMEF周長最小,理由見解析.
時,四邊形PMEF周長最小,理由見解析.
【解析】
試題分析:(1)利用待定系數法求出拋物線的解析式;
(2)首先求出四邊形MEFP面積的表達式,然后利用二次函數的性質求出最值及點P坐標;
(3)四邊形PMEF的四條邊中,PM、EF長度固定,因此只要ME+PF最小,則PMEF的周長將取得最小值.如答圖3所示,將點M向右平移1個單位長度(EF的長度),得M1(1,1);作點M1關于x軸的對稱點M2,則M2(1,﹣1);連接PM2,與x軸交于F點,此時ME+PF=PM2最小.
試題解析:方法一:
試題解析:(1)∵對稱軸為直線x=2,
∴設拋物線解析式為y=a(x﹣2)2+k.
將A(﹣1,0),C(0,5)代入得:![]() ,解得
,解得![]() ,
,
∴y=﹣(x﹣2)2+9=﹣x2+4x+5.
(2)當a=1時,E(1,0),F(2,0),OE=1,OF=2.
設P(x,﹣x2+4x+5),
如答圖2,過點P作PN⊥y軸于點N,則PN=x,ON=﹣x2+4x+5,
∴MN=ON﹣OM=﹣x2+4x+4.
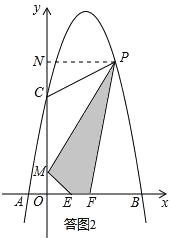
S四邊形MEFP=S梯形OFPN﹣S△PMN﹣S△OME
=![]() (PN+OF)ON﹣
(PN+OF)ON﹣![]() PNMN﹣
PNMN﹣![]() OMOE
OMOE
=![]() (x+2)(﹣x2+4x+5)﹣
(x+2)(﹣x2+4x+5)﹣![]() x(﹣x2+4x+4)﹣
x(﹣x2+4x+4)﹣![]() ×1×1
×1×1
=﹣x2+![]() x+
x+![]()
=﹣(x﹣![]() )2+
)2+![]()
∴當x=![]() 時,四邊形MEFP的面積有最大值為
時,四邊形MEFP的面積有最大值為![]() ,
,
把x=![]() 時,y=﹣(
時,y=﹣(![]() ﹣2)2+9=
﹣2)2+9=![]() .
.
此時點P坐標為(![]() ,
,![]() ).
).
(3)∵M(0,1),C(0,5),△PCM是以點P為頂點的等腰三角形,
∴點P的縱坐標為3.
令y=﹣x2+4x+5=3,解得x=2±![]() .
.
∵點P在第一象限,∴P(2+![]() ,3).
,3).
四邊形PMEF的四條邊中,PM、EF長度固定,因此只要ME+PF最小,則PMEF的周長將取得最小值.
如答圖3,將點M向右平移1個單位長度(EF的長度),得M1(1,1);
作點M1關于x軸的對稱點M2,則M2(1,﹣1);
連接PM2,與x軸交于F點,此時ME+PF=PM2最小.
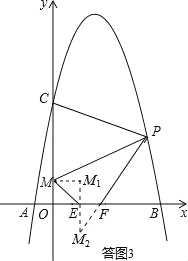
設直線PM2的解析式為y=mx+n,將P(2+![]() ,3),M2(1,﹣1)代入得:
,3),M2(1,﹣1)代入得:
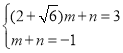 ,解得:m=
,解得:m=![]() ,n=﹣
,n=﹣![]() ,
,
∴y=![]() x﹣
x﹣![]() .
.
當y=0時,解得x=![]() .∴F(
.∴F(![]() ,0).
,0).
∵a+1=![]() ,∴a=
,∴a=![]() .
.
∴a=![]() 時,四邊形PMEF周長最小.
時,四邊形PMEF周長最小.
方法二:
(1)略.
(2)連接MF,過點P作x軸垂線,交MF于點H,
顯然當S△PMF有最大值時,四邊形MEFP面積最大.
當a=1時,E(1,0),F(2,0),
∵M(0,1),
∴lMF:y=﹣![]() x+1,
x+1,
設P(t,﹣t2+4t+5),H(t,﹣![]() t+1),
t+1),
∴S△PMF=![]() (PY﹣HY)(FX﹣MX),
(PY﹣HY)(FX﹣MX),
∴S△PMF=![]() (﹣t2+4t+5+
(﹣t2+4t+5+![]() t﹣1)(2﹣0)=﹣t2+
t﹣1)(2﹣0)=﹣t2+![]() t+4,
t+4,
∴當t=![]() 時,S△PMF最大值為
時,S△PMF最大值為![]() ,
,
∵S△MEF=![]() EF×MY=
EF×MY=![]() ×1×1=
×1×1=![]() ,
,
∴S四邊形MEFP的最大值為![]() +
+![]() =
=![]() .
.
(3)∵M(0,1),C(0,5),△PCM是以點P為頂點的等腰三角形,
∴點P的縱坐標為3,∴﹣x2+4x+5=0,解得:x=2±![]() ,
,
∵點P在第一象限,∴P(2+![]() ,3),PM、EF長度固定,
,3),PM、EF長度固定,
當ME+PF最小時,PMEF的周長取得最小值,
將點M向右平移1個單位長度(EF的長度),得M1(1,1),
∵四邊形MEFM1為平行四邊形,
∴ME=M1F,
作點M1關于x軸的對稱點M2,則M2(1,﹣1),
∴M2F=M1F=ME,
當且僅當P,F,M2三點共線時,此時ME+PF=PM2最小,
∵P(2+![]() ,3),M2(1,﹣1),F(a+1,0),
,3),M2(1,﹣1),F(a+1,0),
∴KPF=KM1F,∴![]() ,∴a=
,∴a=![]() .
.


 藍天教育暑假優化學習系列答案
藍天教育暑假優化學習系列答案科目:初中數學 來源: 題型:
【題目】 下列事件中,屬于必然事件的是( )
A. “世界杯新秀”姆巴佩發點球 100%進球
B. 任意購買一張車票,座位剛好挨著窗口
C. 三角形內角和為 180°
D. 敘利亞不會發生戰爭
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,正方形ABCD的邊長為10 cm,點E,F,G,H分別從點A,B,C,D出發,以2 cm/s的速度同時分別向點B,C,D,A運動.
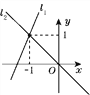
(1)在運動的過程中,四邊形EFGH是何種四邊形?請說明理由.
(2)運動多少秒后,四邊形EFGH的面積為52cm2?
查看答案和解析>>
科目:初中數學 來源: 題型:
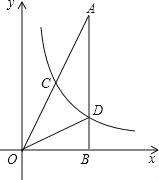
【題目】如圖,在△AOB中,∠ABO=90°,OB=4,AB=8,反比例函數y=![]() 在第一象限內的圖象分別交OA,AB于點C和點D,且△BOD的面積S△BOD=4.
在第一象限內的圖象分別交OA,AB于點C和點D,且△BOD的面積S△BOD=4.
(1)求反比例函數解析式;
(2)求點C的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列說法錯誤的是( )
A. 一個正數的算術平方根一定是正數 B. 一個數的立方根一定比這個數小
C. 一個非零的數的立方根任然是一個非零的數 D. 負數沒有平方根,但有立方根
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com