【題目】計算題
（1）計算： 
（ 
﹣ ）﹣ 
﹣| 
﹣3|
（2）計算：（﹣1）2014﹣ 
sin45°+（π﹣3.14）0
（3）解方程：2x2+x﹣6=0．
【答案】
（1）解：原式= 
﹣3﹣2 + ﹣3
=﹣6
（2）解：原式=1﹣3 
× 
+1
=1﹣3+1
=﹣1
（3）解：（2x﹣3）（x+2）=0，
2x﹣3=0或x+2=0，
所以x1= 
，x2=﹣2
【解析】（1）第一步先進行二次根式的乘法運算、化簡、去掉絕對值符號，第二步合并同類二次根式。
（2）先算乘方開方運算，再算乘法，最后算加減法。
（3）方程的左邊可分解因式，右邊為0，采用因式分解法解方程。
【考點精析】解答此題的關鍵在于理解零指數冪法則的相關知識，掌握零次冪和負整數指數冪的意義： a0=1（a≠0）;a-p=1/ap（a≠0，p為正整數），以及對二次根式的混合運算的理解，了解二次根式的混合運算與實數中的運算順序一樣，先乘方，再乘除，最后加減，有括號的先算括號里的（或先去括號）．
名校課堂系列答案科目：初中數學 來源： 題型：
【題目】如圖 1 是一個長為 4a、寬為 b 的長方形，沿圖中虛線用剪刀平均分成四塊小長方形，然后用四塊小長方形拼成的一個“回形”正方形（如圖 2）．
（1）圖 2 中的陰影部分的面積為 ；（用 a、b 的代數式表示）
（2）觀察圖 2 請你寫出a b2 、a b2 、ab 之間的等量關系是 ；
（3）根據⑵中的結論，若 x y 5 ， x y 
，則 x y2 =_______.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，等腰△ABC的底邊BC=20，面積為120，點F在邊BC上，且BF=3FC，EG是腰AC的垂直平分線，若點D在EG上運動，則△CDF周長的最小值為__．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖,已知△ABD和△ACD關于直線AD對稱；在射線AD上取點E,連接BE, CE,如圖:在射線AD上取點F連接BF, CF,如圖,依此規律，第n個圖形中全等三角形的對數是（ ）
A.nB.2n-1C.
D.3(n+1)
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在△ABC中，∠BAC=100°，∠ABC=∠ACB，點D在直線BC上運動（不與點B、C重合），點E在射線AC上運動，且∠ADE=∠AED，設∠DAC=n．
（1）如圖（1），當點D在邊BC上時，且n=36°，則∠BAD= _________，∠CDE= _________.
（2）如圖（2），當點D運動到點B的左側時，其他條件不變，請猜想∠BAD和∠CDE的數量關系，并說明理由.
（3）當點D運動到點C的右側時，其他條件不變，∠BAD和∠CDE還滿足（2）中的數量關系嗎？請畫出圖形，并說明理由.
查看答案和解析>>
科目：初中數學 來源： 題型：
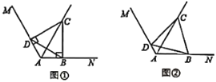
【題目】已知射線AC是∠MAN的角平分線， ∠NAC=60°, B, D分別是射線AN. AM上的點，連接BD.
(1)在圖①中，若∠ABC=∠ADC=90°,求∠CDB的大小；
(2)在圖②中，若∠ABC+∠ADC=180°,求證：四邊形ABCD的面積是個定值.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，為了測量樓的高度，自樓的頂部A看地面上的一點B，俯角為30°，已知地面上的這點與樓的水平距離BC為30m，那么樓的高度AC為m（結果保留根號）．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
