【題目】如圖，在Rt△ABC中，∠ACB＝90°，將△ABC繞頂點C逆時針旋轉得到△A′B′C，M是BC的中點，P是A′B′的中點，連接PM，若BC＝2，∠BAC＝30°，則線段PM的最大值是_____．
科目：初中數學 來源： 題型：
【題目】閱讀下列材料并解決問題
進位制是一種記數方式，可以用有限的數字符號代表所有的數值，使用數字符號的數目稱為基數，基數為n，即可稱n進制。現在最常用的是十進制，通常使用10個阿拉伯數字0~9進行記數，特點是逢十進一。
對于任意一個用
進制表示的數，通常使用n個阿拉伯數字
進行記數，特點是逢n進一。我們可以通過以下方式把它轉化為十進制：
例如：五進制數
，記作: 
，
七進制數
，記作: 
（1）請將以下兩個數轉化為十進制： 
____________， 
____________ ；
（2）若一個正數可以用七進制表示為
，也可以用五進制表示為
，請求出這個數并用十進制表示。
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知：如圖，點C在∠AOB的一邊OA上，過點C的直線DE∥OB，CF平分∠ACD，CG⊥CF于點C．
(1)若∠O＝40°，求∠ECF的度數；
(2)求證：CG平分∠OCD．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】列方程組解應用題
5月份，甲、乙兩個工廠用水量共為200噸．進入夏季用水高峰期后，兩工廠積極響應國家號召，采取節水措施.6月份，甲工廠用水量比5月份減少了15%，乙工廠用水量比5月份減少了10%，兩個工廠6月份用水量共為174噸，求兩個工廠5月份的用水量各是多少?
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在
中，
，點
從點
出發沿
方向以
的速度向點
勻速運動，同時點
從點出發沿
方向以
的速度向點
勻速運動，當其中一個點到達終點時，另一個點也隨之停止運動．設點
運動的時間是
.過點作
于點
連結
（1）求證：
；
（2）四邊形
能夠成為菱形嗎？如果能，求出相應的
值，如果不能，說明理由；
（3）當為何值時，
為直角三角形？請說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在△ABC中，AB＝AC，以AB為直徑的⊙O分別與BC，AC交于點D，E，過點D作DF⊥AC于點F.
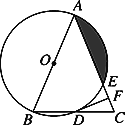
(1)判斷DF與是⊙O的位置關系，并證明你的結論。
(2)若⊙O的半徑為4，∠CDF＝22.5°，求陰影部分的面積．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知，在三角形ABC中，點D在BC上，DE⊥AB于E，點F在AB上，在CF的延長線上取一點G，連接AG.
(1)如圖1,若∠GAB=∠B,∠GAC+∠EDB=180°，求證：AB⊥AC.
(2)如圖2.在(1)的條件下,∠GAC的平分線交CG于點M,∠ACB的平分線交AB于點N,當∠AMC∠ANC=35°時，求∠AGC的度數。
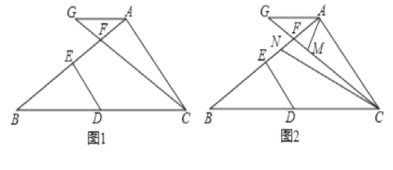
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，一塊長和寬分別為60厘米和40厘米的長方形鐵皮，要在它的四角截去四個相等的小正方形，折成一個無蓋的長方體水槽，使它的底面積為800平方厘米.求截去正方形的邊長.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】現有兩個可以自由轉動的轉盤，每個轉盤分成三個相同的扇形，涂色情況如圖所示，指針的位置固定，同時轉動兩個轉盤，回答以下問題：
圓1 圓2
圓2 圓1 | |||
(1)補全表格：圓1的所有可能結果有 種，分別是 ；
圓2的所有可能結果有 種，分別是 .
(2)寫出：轉盤停止后指針指向同種顏色區域的概率和至少有一指針指向紅色區域的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
