
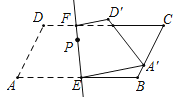
【題目】如圖,直線EF分別交平行四邊形ABCD邊AB、CD于直E、F,將圖形沿直線EF對折,點A、D分別落在點A′、D′處.若∠A=60°,AD=4,AB=8,當點A′落在BC邊上任意點時,設點P為直線EF上的動點,請直接寫出PC+PA′的最小值( )
A.4+![]() B.8C.6+
B.8C.6+![]() D.4
D.4![]()
【答案】D
【解析】
連接AC交EF于P′,連接P′A′,作CH⊥AB交AB的延長線于H.因為A、A′關于直線EF對稱,推出P′A′=P′A,推出P′A′+P′C=P′A+P′C=AC,推出當點P與P′重合時,PA′+PC的值最小,最小值=AC的長;
如圖,連接AC交EF于P′,連接P′A′,作CH⊥AB交AB的延長線于H.
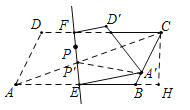
∵A、A′關于直線EF對稱,
∴P′A′=P′A,
∴P′A′+P′C=P′A+P′C=AC,
∴當點P與P′重合時,PA′+PC的值最小,最小值=AC的長.
在Rt△BCH中,∵BC=4,∠CBH=60°,
∴BH=2,CH=2![]() ,
,
∴AH=AB+BH=10,
在Rt△ACH中,AC=![]() .
.
∴PC+PA′的最小值為![]() ,
,
故選:D.


 一線名師提優試卷系列答案
一線名師提優試卷系列答案科目:初中數學 來源: 題型:
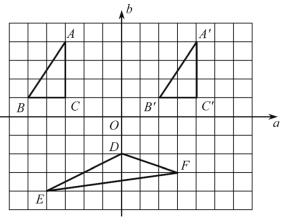
【題目】在如圖所示的方格圖中,我們稱每個小正方形的頂點為“格點”,以格點為頂點的三角形叫做“格點三角形”,根據圖形,回答下列問題.
(1)圖中格點三角形A′B′C′是由格點三角形ABC通過怎樣的變換得到的?
(2)如果以直線a,b為坐標軸建立平面直角坐標系后,點A的坐標為(-3,4),請求出三角形DEF的面積S.
查看答案和解析>>
科目:初中數學 來源: 題型:
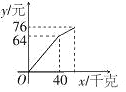
【題目】小明在暑期社會實踐活動中,以每千克0.8元的價格從批發市場購進若干千克西瓜到市場上去銷售,在銷售了40千克西瓜之后,余下的每千克降價0.4元,全部售完.銷售金額與售出西瓜的千克數之間的關系如圖所示.請你根據圖象提供的信息完成以下問題:
(1)求降價前銷售金額y(元)與售出西瓜x(千克)之間的函數關系式.
(2)小明從批發市場共購進多少千克西瓜?
(3)小明這次賣瓜賺了多少錢?
查看答案和解析>>
科目:初中數學 來源: 題型:
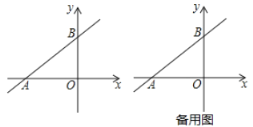
【題目】如圖,直線![]() 與
與![]() 軸,
軸,![]() 軸分別交于
軸分別交于![]() ,
,![]() 兩點,且經過點
兩點,且經過點![]() .
.
(1)求![]() 的值;
的值;
(2)若![]() ,
,
①求![]() 的值;
的值;
②點![]() 為
為![]() 軸上一動點,點
軸上一動點,點![]() 為坐標平面內另一點,若以
為坐標平面內另一點,若以![]() ,
,![]() ,
,![]() ,
,![]() 為頂點的四邊形是菱形,請直接寫出所有符合條件的點
為頂點的四邊形是菱形,請直接寫出所有符合條件的點![]() 的坐標.
的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,ABCD中,對角線AC和BD相交于點O,如果AC=12、BD=10、AB=m,那么m的取值范圍是( )
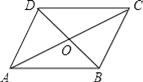
A. 1<m<11 B. 2<m<22 C. 10<m<12 D. 5<m<6
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】南山植物園中現有A、B兩個園區,已知A園區為長方形,長為(x+y)米,寬為(x﹣y)米;B園區為正方形,邊長為(x+3y)米.
(1)請用代數式表示A、B兩園區的面積之和并化簡;
(2)現根據實際需要對A園區進行整改,長增加(11x﹣y)米,寬減少(x﹣2y)米,整改后A區的長比寬多350米,且整改后兩園區的周長之和為980米.
①求x、y的值;
②若A園區全部種植C種花,B園區全部種植D種花,且C、D兩種花投入的費用與吸引游客的收益如表:

求整改后A、B兩園區旅游的凈收益之和.(凈收益=收益﹣投入)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB是⊙O的直徑,點C在AB的延長線上,CD與⊙O相切于點D,CE⊥AD,交AD的延長線于點E.
(1)求證:∠BDC=∠A;
(2)若CE=2,DE=1,求AD的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在正方形ABCD中,AC為對角線,E為AB上一點,過點E作EF∥AD,與AC,DC分別交于點G,F,H為CG的中點,連接DE,EH,DH,FH.下列結論中結論正確的有( )
①EG=DF;
②∠AEH+∠ADH=180°;
③△EHF≌△DHC;
④若 ![]() =
= ![]() ,則S△EDH=13S△CFH .
,則S△EDH=13S△CFH . 
A.1個
B.2個
C.3個
D.4個
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com