
【題目】如圖,AB是⊙O的直徑,點C,D是半圓O的三等分點,過點C作⊙O的切線交AD的延長線于點E,過點D作DF⊥AB于點F,交⊙O于點H,連接DC,AC. 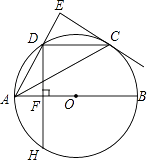
(1)求證:∠AEC=90°;
(2)試判斷以點A,O,C,D為頂點的四邊形的形狀,并說明理由;
(3)若DC=2,求DH的長.
【答案】
(1)證明:連接OC,

∵EC與⊙O切點C,
∴OC⊥EC,
∴∠OCE=90°,
∵點CD是半圓O的三等分點,
∴ ![]() =
= ![]() =
= ![]() ,
,
∴∠DAC=∠CAB,
∵OA=OC,
∴∠CAB=∠OCA,
∴∠DAC=∠OCA,
∴AE∥OC(內錯角相等,兩直線平行)
∴∠AEC+∠OCE=180°,
∴∠AEC=90°
(2)解:四邊形AOCD為菱形.
理由是:
∵ ![]() =
= ![]() ,
,
∴∠DCA=∠CAB,
∴CD∥OA,
又∵AE∥OC,
∴四邊形AOCD是平行四邊形,
∵OA=OC,
∴平行四邊形AOCD是菱形(一組鄰邊相等的平行四邊形是菱形)
(3)解:連接OD.

∵四邊形AOCD為菱形,
∴OA=AD=DC=2,
∵OA=OD,
∴OA=OD=AD=2,
∴△OAD是等邊三角形,
∴∠AOD=60°,
∵DH⊥AB于點F,AB為直徑,
∴DH=2DF,
在Rt△OFD中,sin∠AOD= ![]() ,
,
∴DF=ODsin∠AOD=2sin60°= ![]() ,
,
∴DH=2DF=2 ![]() .
.
【解析】(1)連接OC,根據EC與⊙O切點C,則∠OCE=90°,由題意得 ![]() =
= ![]() =
= ![]() ,∠DAC=∠CAB,即可證明AE∥OC,則∠AEC+∠OCE=180°,從而得出∠AEC=90°;(2)四邊形AOCD為菱形.由(1)得
,∠DAC=∠CAB,即可證明AE∥OC,則∠AEC+∠OCE=180°,從而得出∠AEC=90°;(2)四邊形AOCD為菱形.由(1)得 ![]() =
= ![]() ,則∠DCA=∠CAB可證明四邊形AOCD是平行四邊形,再由OA=OC,即可證明平行四邊形AOCD是菱形(一組鄰邊相等的平行四邊形是菱形);(3)連接OD.根據四邊形AOCD為菱形,得△OAD是等邊三角形,則∠AOD=60°,再由DH⊥AB于點F,AB為直徑,在Rt△OFD中,根據sin∠AOD=
,則∠DCA=∠CAB可證明四邊形AOCD是平行四邊形,再由OA=OC,即可證明平行四邊形AOCD是菱形(一組鄰邊相等的平行四邊形是菱形);(3)連接OD.根據四邊形AOCD為菱形,得△OAD是等邊三角形,則∠AOD=60°,再由DH⊥AB于點F,AB為直徑,在Rt△OFD中,根據sin∠AOD= ![]() ,求得DH的長.
,求得DH的長.
【考點精析】認真審題,首先需要了解切線的性質定理(切線的性質:1、經過切點垂直于這條半徑的直線是圓的切線2、經過切點垂直于切線的直線必經過圓心3、圓的切線垂直于經過切點的半徑),還要掌握解直角三角形(解直角三角形的依據:①邊的關系a2+b2=c2;②角的關系:A+B=90°;③邊角關系:三角函數的定義.(注意:盡量避免使用中間數據和除法))的相關知識才是答題的關鍵.


科目:初中數學 來源: 題型:
【題目】如圖,EF過□ABCD對角線的交點O,交AD于E,交BC于F,若□ ABCD的周長為16,OE=2.5,則四邊形EFCD的周長為( )
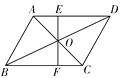
A. 10 B. 11 C. 12 D. 13
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠ACB=90°,過點C的直線MN∥AB,D為AB邊上一點,過點D作DE⊥BC,交直線MN于點E,垂足為F,連接CD,BE
(1)求證:CE=AD
(2)若D為AB的中點,則∠A的度數滿足什么條件時,四邊形BECD是正方形?請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,E是矩形ABCD內的一個動點,連接EA、EB、EC、ED,得到△EAB、△EBC、△ECD、△EDA,設它們的面積分別是m、n、p、q,給出如下結論:
①m+n=q+p;
②m+p=n+q;
③若m=n,則E點一定是AC與BD的交點;
④若m=n,則E點一定在BD上.
其中正確結論的序號是( )

A. ①③ B. ②④ C. ①②③ D. ②③④
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com