
(本題滿分12分,第(1)題7分,第(2)題5分)
如圖,在⊙O中,直徑AB與弦CD垂直,垂 足為E,連接AC,將△ACE沿AC翻折得到△ACF,直線FC與直線AB相交于點G.
足為E,連接AC,將△ACE沿AC翻折得到△ACF,直線FC與直線AB相交于點G.
(1)證明:直線FC與⊙O相切;
(2)若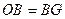 ,求證:四邊形OCBD是菱形.
,求證:四邊形OCBD是菱形.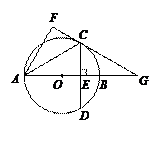

解:(1)連接 . ………………………………………1分
. ………………………………………1分

∵ , ∴
, ∴ …………………………………………1分
…………………………………………1分
由翻折得, ,
, .…1分
.…1分
∴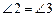 . …………………………………1分
. …………………………………1分
∴OC∥AF.……………………………………1分
∴ .…………………………1分
.…………………………1分
∵點C在圓上
∴直線FC與⊙O相切.………………………1分
(2)解一:在Rt△OCG中,∵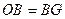 ,∴
,∴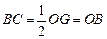 , …………1分
, …………1分
∵直徑AB垂直弦CD,  ∴
∴
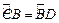 ………………………1分
………………………1分
∴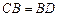 ………………………1分
………………………1分
∵
∴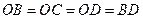 . ………………………1分
. ………………………1分
∴四邊形OCBD是菱形. ………………………1分
解二:在Rt△OCG中,∵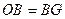 ,∴
,∴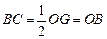 ,………………1分
,………………1分
∵ ,∴
,∴ ………………………1分
………………………1分
∵AB垂直于弦 CD, ∴
CD, ∴ ………………………1分
………………………1分
∵直徑AB垂直弦CD, ∴ ………………………1分
………………………1分
∴四邊形OCBD是平行四邊形
∵AB垂直于弦CD,∴四邊形OCBD是菱形.…………………………………1分
解析


 開心蛙口算題卡系列答案
開心蛙口算題卡系列答案科目:初中數學 來源: 題型:
 的
的 與x軸交于
與x軸交于 、
、 兩點,且點C在x軸的上方.
兩點,且點C在x軸的上方.

 、B、C,求這二次函數的解析式;
、B、C,求這二次函數的解析式;查看答案和解析>>
科目:初中數學 來源:2011屆上海市普陀區4月中考模擬數學試卷 題型:解答題
(本題滿分12分,第(1)小題4分,第(2)小題4分、第(3)小題4分)
如圖8,在平面直角坐標系xOy中,半徑為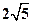 的
的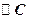 與x軸交于
與x軸交于 、
、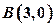 兩點,且點C在x軸的上方.
兩點,且點C在x軸的上方.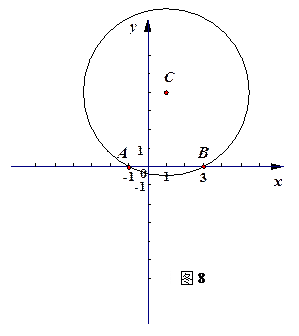

(1)求圓心C的坐標;
(2)已知一個二次函數的圖像經過點 、B、C,求這二次函數的解析式;
、B、C,求這二次函數的解析式;
(3)設點P在y軸上,點M在(2)的二次函數圖像上,如果以點P、 M、A、B為頂點的四邊形是平行四邊形,請你直接寫出點M的坐標.
M、A、B為頂點的四邊形是平行四邊形,請你直接寫出點M的坐標.
查看答案和解析>>
科目:初中數學 來源:2011屆上海市普陀區4月中考模擬數學試卷 題型:解答題
(本題滿分12分,第(1)小題滿分6分,第(2)小題滿分6分)如圖7,等腰三角形ABC中,AB=AC,AH垂直BC,點E是AH上一點,延長AH至點F,使FH=EH,
(1)求證:四邊形EBFC是菱形;
(2)如果 =
= ,求證:
,求證: .
.

查看答案和解析>>
科目:初中數學 來源:2010-2011學年上海市徐匯區初三年級數學學科學習能力診斷試卷 題型:解答題
(本題滿分12分,第(1)、(2)題各6分)
如圖,已知拋物線y=ax2+bx+c與x軸交于A、B兩點,與y軸交于點C, D為OC的中點,直線AD交拋物線于點E(2,6),且△ABE與△ABC的面積之比為3∶2.
(1)求直線AD和拋物線的解析式;
(2)拋物線的對稱軸與 軸相交于點F,點Q為直線AD上一點,且△ABQ與△ADF相似,直接寫出點Q點的坐標.
軸相交于點F,點Q為直線AD上一點,且△ABQ與△ADF相似,直接寫出點Q點的坐標.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com