
【題目】如圖,已知ABCD中,AE⊥BC于點E,以點B為中心,取旋轉角等于∠ABC,把△BAE順時針旋轉,得到△BA′E′,連接DA′.若∠ADC=60°,∠ADA′=50°,則∠DA′E′的大小為( )
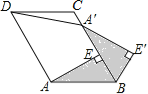
A. 130° B. 150° C. 160° D. 170°
科目:初中數學 來源: 題型:
【題目】甲、乙兩人在筆直的道路![]() 上相向而行,甲騎自行車從
上相向而行,甲騎自行車從![]() 地到
地到![]() 地,乙駕車從
地,乙駕車從![]() 地到
地到![]() 地,假設他們分別以不同的速度勻速行駛,甲先出6分鐘后,乙才出發,乙的速度為
地,假設他們分別以不同的速度勻速行駛,甲先出6分鐘后,乙才出發,乙的速度為![]() 千米/分,在整個過程中,甲、乙兩人之間的距離
千米/分,在整個過程中,甲、乙兩人之間的距離![]() (千米)與甲出發的時間
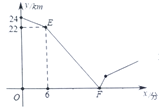
(千米)與甲出發的時間![]() (分)之間的部分函數圖象如圖.
(分)之間的部分函數圖象如圖.
(1)![]() 兩地相距______千米,甲的速度為______千米/分;
兩地相距______千米,甲的速度為______千米/分;
(2)直接寫出點![]() 的坐標______,求線段
的坐標______,求線段![]() 所表示的
所表示的![]() 與
與![]() 之間的函數表達式;
之間的函數表達式;
(3)當乙到達終點![]() 時,甲還需______分鐘到達終點
時,甲還需______分鐘到達終點![]() .
.
查看答案和解析>>
科目:初中數學 來源: 題型:
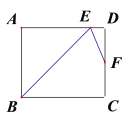
【題目】如圖,在矩形ABCD中,∠B的平分線BE與AD交于點E,∠BED的平分線EF與DC交于點F,當點F是CD的中點時,若AB=4,則BC=_________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在直角坐標系中,反比例函數y=![]() (x>0),過點A(3,4).
(x>0),過點A(3,4).
(1)求y關于x的函數表達式.
(2)求當y≥2時,自變量x的取值范圍.
(3)在x軸上有一點P(1,0),在反比例函數圖象上有一個動點Q,以PQ為一邊作一個正方形PQRS,當正方形PQRS有兩個頂點在坐標軸上時,畫出狀態圖并求出相應S點坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
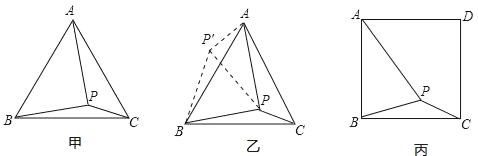
【題目】如圖甲,在等邊三角形ABC內有一點P,且PA=2,PB=![]() ,PC=1,求∠BPC度數的大小和等邊三角形ABC的邊長.
,PC=1,求∠BPC度數的大小和等邊三角形ABC的邊長.
解題思路是:將△BPC繞點B逆時針旋轉60°,如圖乙所示,連接PP′.
(1)△P′PB是 三角形,△PP′A是 三角形,∠BPC= °;
(2)利用△BPC可以求出△ABC的邊長為 .
如圖丙,在正方形ABCD內有一點P,且PA=![]() ,BP=
,BP=![]() ,PC=1;
,PC=1;
(3)求∠BPC度數的大小;
(4)求正方形ABCD的邊長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點A從原點O出發沿數軸向左運動,同時,點B也從原點出發沿數軸向右運動,5秒后,兩點相距15個單位長度,已知點B的速度是點A的速度的2倍(速度單位:單位長度/秒)
![]()
(1)求出點A、點B運動的速度;并在數軸上標出A、B兩點從原點O出發運動5秒時的位置.
(2)若A、B兩點從(1)中的位置開始,仍以原來的速度同時沿數軸向左運動,
①再過幾秒,A、B兩點重合?
②再過幾秒,可以讓A、B、O三點中一點是另外兩點所成線段的中點?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】補全解題過程.
已知:如圖,O是直線AB上的一點,∠COD=90°,OE平分∠BOC.若∠AOC=60°,求∠DOE數.
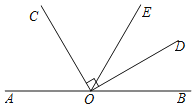
解:∵O是直線AB上的一點,(已知)
∴∠BOC=180°﹣∠AOC.(_________)
∵∠AOC=60°,(已知)
∴∠BOC=120°.(_________)
∵OE平分∠BOC,(已知)
∴∠COE=![]() ∠BOC,(_________)
∠BOC,(_________)
∴∠COE=_____°.
∵∠DOE=∠COD﹣∠COE,且∠COD=90°,
∴∠DOE=_____°.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】李叔叔在“中央山水”買了一套經濟適用房,他準備將地面鋪上地磚,這套住宅的建筑平面(由四個長方形組成)如圖所示(圖中長度單位:米),請解答下問題:
(1)用式子表示這所住宅的總面積;
(2)若鋪1平方米地磚平均費用120元,求當x=6時,這套住宅鋪地磚總費用為多少元?
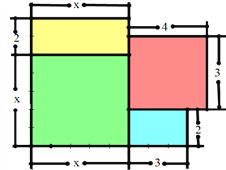
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】“文明城市,你我共建”一起助力太原市創建全國文明城市.下面是某校“數學之星”課外興趣小組的同學們,在對![]() 個自行車騎行規則進行調查時設計的問卷,
個自行車騎行規則進行調查時設計的問卷,
自行車騎行規則知多少
您好:
我們來自課外興趣小組,為了了解我市市民騎行自行車的安全意識,請您抽出一點時間填寫這份問卷。謝謝合作!
規則1 不準在機動車道內騎行.( )
A.知道 B.不知道
規則2 不準闖紅燈.( )
A知道 B.不知道
規則3 不準騎車帶人.( )
A.知道 B.不知道
規則4 橫過人行橫道時不準騎行.( )
A.知道 B.不知道
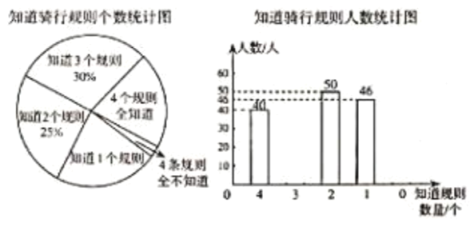
小組的同學們]隨機抽取了部分市民進行調查,并將結果制成了如下兩幅不完整的統計圖.
請根據統計圖解答下列問題:
![]() 求被調查的市民人數;
求被調查的市民人數;
![]() 在扇形統計圖中,求“
在扇形統計圖中,求“![]() 個規則全知道”所對圓心角的度數;
個規則全知道”所對圓心角的度數;
![]() 請補全條形統計圖;
請補全條形統計圖;
![]() 請根據調查結果,談談你的看法.
請根據調查結果,談談你的看法.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com