
【題目】小紅同學要測量A、C兩地的距離,但A、C之間有一水池,不能直接測量,于是她在A、C同一水平面上選取了一點B,點B可直接到達A、C兩地.她測量得到AB=80米,BC=20米,∠ABC=120°.請你幫助小紅同學求出A、C兩點之間的距離.(參考數據 ![]() ≈4.6)
≈4.6)
科目:初中數學 來源: 題型:
【題目】兩條直線被第三條直線所截,若∠1與∠2 是同旁內角,且∠1=70,則 ( )
A. ∠2=70B. ∠2=110
C. ∠2=70或∠2=110D. ∠2的度數不能確定
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知BD是矩形ABCD的對角線. 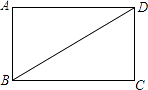
(1)用直尺和圓規作線段BD的垂直平分線,分別交AD、BC于E、F(保留作圖痕跡,不寫作法和證明).
(2)連結BE,DF,問四邊形BEDF是什么四邊形?請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某班體育課上,老師測試10個同學做引體向上的成績,10個同學的成績記錄見下表:
引體向上的個數 | 5 | 6 | 7 |
人數 | 3 | 4 | 3 |
則這10個同學做引體向上的成績的平均數是( )
A. 4 B. 5 C. 6 D. 7
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】幾何計算:
如圖,已知∠AOB=40°,∠BOC=3∠AOB,OD平分∠AOC,求∠COD的度數.
解:因為∠BOC=3∠AOB,∠AOB=40°
所以∠BOC=__________°
所以∠AOC=__________ + _________
=__________° + __________°
=__________°
因為OD平分∠AOC
所以∠COD=![]() __________=__________°
__________=__________°

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AD是BC邊上的中線,E是AD的中點,過點A作BC的平行線交BE的延長線于點F,連接CF. 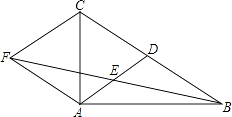
(1)求證:AF=DC;
(2)若AB⊥AC,試判斷四邊形ADCF的形狀,并證明你的結論.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,OE是∠AOD的平分線,OC是∠BOD的平分線.
(1)若∠AOB=130°,則∠COE是多少度?
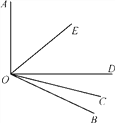
(2)在(1)的條件下,若∠COD=20°,則∠BOE是多少度?
查看答案和解析>>
科目:初中數學 來源: 題型:
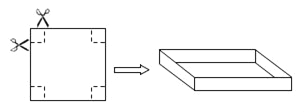
【題目】把一邊長為40cm的正方形硬紙板,進行適當的剪裁,折成一個長方形盒子(紙板的厚度忽略不計)。
(1)如圖,若在正方形硬紙板的四角各剪一個同樣大小的正方形,將剩余部分折成一個無蓋的長方形盒子。
①要使折成的長方形盒子的底面積為484cm2,那么剪掉的正方形的邊長為多少?
②折成的長方形盒子的側面積是否有最大值?如果有,求出這個最大值和此時剪掉的正方形的邊長;如果沒有,說明理由。
(2)若在正方形硬紙板的四周剪掉一些矩形(即剪掉的矩形至少有一條邊在正方形硬紙板的邊上),將剩余部分折成一個有蓋的長方形盒子,若折成的一個長方形盒子的表面積為550cm2,求此時長方形盒子的長、寬、高(只需求出符合要求的一種情況)。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com