
【題目】如圖①,一個正方體鐵塊放置在圓柱形水槽內,現以一定的速度往水槽中注水,28s時注滿水槽.水槽內水面的高度y(cm)與注水時間x(s)之間的函數圖象如圖②所示.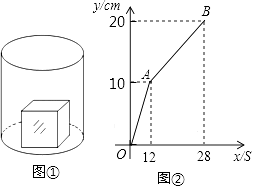
(1)正方體的棱長為cm;
(2)求線段AB對應的函數解析式,并寫出自變量x的取值范圍;
(3)如果將正方體鐵塊取出,又經過t(s)恰好將此水槽注滿,直接寫出t的值.
【答案】
(1)由題意可得:12秒時,水槽內水面的高度為10cm,12秒后水槽內高度變化趨勢改變,故正方體的棱長為10cm;故答案為:10;
(2)解:設線段AB對應的函數解析式為:y=kx+b,
∵圖象過A(12,10),B(28,20),
∴ ![]() ,
,
解得: ![]() ,
,
∴線段AB對應的解析式為:y= ![]() x+
x+ ![]() (12≤x≤28);
(12≤x≤28);
(3)解:∵28﹣12=16(s),
∴沒有立方體時,水面上升10cm,所用時間為:16秒,
∵前12秒由立方體的存在,導致水面上升速度加快了4秒,
∴將正方體鐵塊取出,經過4秒恰好將此水槽注滿.
【解析】(1)由圖像可知點A是折點,坐標對應的水槽內水面的高度就等于小正方體的棱長;(2)AB段端點坐標均已知,利用待定系數法即可求出;(3)由圖像可知,正方體棱長等于整個圓柱高度的一半,所用時間少下半部分少用4分鐘,就是因為正方體的存在少用了,因此取出正方體后,經過4秒恰好將水槽注滿.


科目:初中數學 來源: 題型:
【題目】為了解食品安全狀況,質監部門抽查了甲、乙、丙、丁四個品牌飲料的質量,將收集的數據整理并繪制成圖1和圖2兩幅尚不完整的統計圖,請根據圖中的信息,完成下列問題: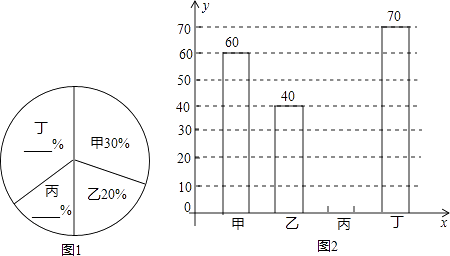
(1)這次抽查了四個品牌的飲料共瓶;
(2)請你在答題卡上補全兩幅統計圖;
(3)若四個品牌飲料的平均合格率是95%,四個品牌飲料月銷售量約15萬瓶,請你估計這四個品牌的不合格飲料有多少瓶?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,CE平分∠ACD,AE平分∠BAC,∠EAC+∠ACE=90°

(1)請判斷AB與CD的位置關系并說明理由;
(2)如圖2,在(1)的結論下,當∠E=90°保持不變,移動直角頂點E,使∠MCE=∠ECD,當直角頂點E點移動時,問∠BAE與∠MCD是否存在確定的數量關系?

(3)如圖3,在(1)的結論下,P為線段AC上一定點,點Q為直線CD上一動點,當點Q在射線CD上運動時(點C除外)∠CPQ+∠CQP與∠BAC有何數量關系? (2、3小題只需選一題說明理由)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知a,b,c滿足|a-![]() |+
|+![]() +(c-
+(c-![]() )2=0.
)2=0.
(1)求a,b,c的值;
(2)試問以a,b,c為邊能否構成三角形?若能,求出其周長;若不能,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知,如圖,∠1=∠ACB,∠2=∠3,FH⊥AB于H,求證:CD⊥AB.
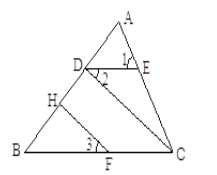
證明:∵∠1=∠ACB(已知)
∴DE∥BC( )
∴∠2= ( )
∵∠2=∠3(已知)
∴∠3=
∴CD∥FH( )
∴∠BDC=∠BHF( )
又∵FH⊥AB(已知)
∴ ( )
∵CD∥FH
∴∠BHF=∠BDC=90°( )
即CD⊥AB( )
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】畫出直線y=![]() x-1的圖象,利用圖象求:
x-1的圖象,利用圖象求:
(1)當x≥2時,y的取值范圍;
(2)當y<0時,x的取值范圍;
(3)當-1≤y≤2時,對應x的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某工廠現在平均每天比原計劃多生產50臺機器,現在生產600臺機器所需要的時間與原計劃生產450臺機器所需要的時間相同.
(1)原計劃平均每天生產多少臺機器?
(2)若該工廠要在不超過5天的時間,生產1100臺機器,則平均每天至少還要再多生產多少臺機器?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某乒乓球館有兩種計費方案,如下圖表.李強和同學們打算周末去此乒乓球館連續打球4小時,經服務生測算后,告知他們包場計費方案會比人數計費方案便宜,則他們參與包場的人數至少為( )
包場計費:包場每場每小時50元,每人須另付入場費5元 |
人數計費:每人打球2小時20元,接著續打球每人每小時6元 |
A. 9B. 8C. 7D. 6
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com