
如圖,在Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm.點D,E,F分別是邊AB,BC,AC的中點,連接DE、DF,動點P,Q分別從點A、B同時出發,運動速度均為1cm/s,點P沿AFD的方向運動到點D停止;點Q沿BC的方向運動,當點P停止運動時,點Q也停止運動.在運動過程中,過點Q作BC的垂線交AB于點M,以點P,M,Q為頂點作平行四邊形PMQN.設平行四邊形邊形PMQN與矩形FDEC重疊部分的面積為y(cm2)(這里規定線段是面積為0的幾何圖形),點P運動的時間為x(s)
(1)當點P運動到點F時,CQ= cm;
(2)在點P從點F運動到點D的過程中,某一時刻,點P落在MQ上,求此時BQ的長度;
(3)當點P在線段FD上運動時,求y與x之間的函數關系式.
(1)5。
(2) (cm)。
(cm)。
(3)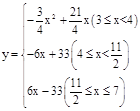 。
。
解析試題分析:(1)當點P運動到點F時,求出AF=FC=3cm,BQ=AF=3cm,即可求出答案。
(2)根據在點P從點F運動到點D的過程中,點P落在MQ上得出方程t+t﹣3=8,求出即可。
(3)求出DE= AC=3,DF=
AC=3,DF= BC=4,證△MBQ∽△ABC,求出MQ=
BC=4,證△MBQ∽△ABC,求出MQ=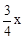 ,分為三種情況:①當3≤x<4時,重疊部分圖形為平行四邊形,根據y=PN•PD代入求出即可;②當4≤x<
,分為三種情況:①當3≤x<4時,重疊部分圖形為平行四邊形,根據y=PN•PD代入求出即可;②當4≤x< 時,重疊部分為矩形,根據圖形得出
時,重疊部分為矩形,根據圖形得出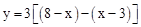 ;③當
;③當 ≤x≤7時,重疊部分圖形為矩形,根據圖形得出
≤x≤7時,重疊部分圖形為矩形,根據圖形得出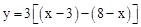 ,求出即可。
,求出即可。
解:(1)當點P運動到點F時,
∵F為AC的中點,AC=6cm,∴AF=FC=3cm。
∵P和Q的運動速度都是1cm/s,∴BQ=AF=3cm。
∴CQ=8cm﹣3cm=5cm。
(2)設在點P從點F運動到點D的過程中,點P落在MQ上,如圖,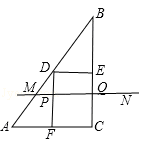
則t+t﹣3=8,∴t= 。
。
∴BQ的長度為 ×1=
×1= (cm)。
(cm)。
(3)∵D、E、F分別是AB、BC、AC的中點,
∴DE= AC=
AC= ×6=3,DF=
×6=3,DF= BC=
BC= ×8=4。
×8=4。
∵MQ⊥BC,∴∠BQM=∠C=90°。
∵∠QBM=∠CBA,∴△MBQ∽△ABC。
∴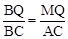 ,即
,即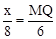 。∴MQ=
。∴MQ=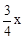 。
。
分為三種情況討論:
①當3≤x<4時,重疊部分圖形為平行四邊形,如圖,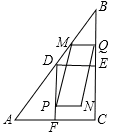
y=PN•PD=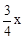 (7﹣x),
(7﹣x),
即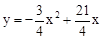 。
。
②當4≤x< 時,重疊部分為矩形,如圖,
時,重疊部分為矩形,如圖,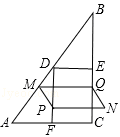
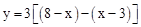 ,
,
即y=﹣6x+33。
③當 ≤x≤7時,重疊部分圖形為矩形,如圖,
≤x≤7時,重疊部分圖形為矩形,如圖,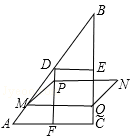
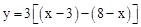 ,
,
即y=6x﹣33。
綜上所述,當點P在線段FD上運動時, y與x之間的函數關系式為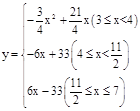 。
。


 手拉手全優練考卷系列答案
手拉手全優練考卷系列答案科目:初中數學 來源: 題型:
| A、16℃≤t≤18℃ | B、16℃≤t≤20℃ | C、16℃≤t≤22℃ | D、18℃≤t≤18℃ |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
某初中學校共有學生720人,該校有關部門從全體學生中隨機抽取了50人,對其到校方式進行調查,并將調查的結果制成了如圖所示的條形統計圖,由此可以估計全校坐公交車到校的學生有 人.
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
丁丁參加了一次智力競賽,共回答了30道題,題目的評分標準是這樣的:答對一題加5分,一題答錯或不答倒扣1分.如果在這次競賽中丁丁的得分要超過100分,那么他至少要答對多少題?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com