
【題目】解分式方程:(1)![]() ;
;
(2)![]() .
.
【答案】(1)x=4;(2)無(wú)解
【解析】
(1)兩邊乘以最簡(jiǎn)公分母(x-2)轉(zhuǎn)化為整式方程,然后求出整式方程的解,再代入最簡(jiǎn)公分母檢驗(yàn)即可得出分式方程的解;
(2)兩邊乘以最簡(jiǎn)公分母(x+1)(x-1)轉(zhuǎn)化為整式方程,然后求出整式方程的解,再代入最簡(jiǎn)公分母檢驗(yàn)即可得出分式方程的解.
解:(1)方程的兩邊同乘(x-2),得:1-x+2(x-2)=1,
解得:x=4.
檢驗(yàn):當(dāng)x=4時(shí),x-2=2≠0,
所以x=4是原分式方程的解;
(2)方程的兩邊同乘(x+1)(x-1),得:(x+1)2-4=(x+1)(x-1),
解得:x=1.
檢驗(yàn):當(dāng)x=1時(shí),(x+1)(x-1)=0,即x=1不是原分式方程的解.
則原方程無(wú)解.


 開心練習(xí)課課練與單元檢測(cè)系列答案
開心練習(xí)課課練與單元檢測(cè)系列答案 開心試卷期末沖刺100分系列答案
開心試卷期末沖刺100分系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,有下列四種結(jié)論:①AB=AD;②∠B=∠D;③∠BAC=∠DAC;④BC=DC.以其中的2個(gè)結(jié)論作為依據(jù)不能判定△ABC≌△ADC的是( )
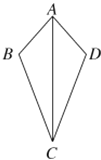
A. ①② B. ①③ C. ①④ D. ②③
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在邊長(zhǎng)為1個(gè)單位長(zhǎng)度的小正方形組成的網(wǎng)格中,給出了格點(diǎn)△ABC(頂點(diǎn)是網(wǎng)格線的交點(diǎn))和格點(diǎn)P.
(1)以A點(diǎn)為位似中心,將△ABC在網(wǎng)格中放大成△AB1C1,使![]() =2,請(qǐng)畫出△AB1C1;
=2,請(qǐng)畫出△AB1C1;
(2)以P點(diǎn)為三角形的一個(gè)頂點(diǎn),請(qǐng)畫一個(gè)格點(diǎn)△PMN,使△PMN∽△ABC,且相似比為![]() .
.
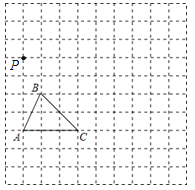
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖1,直線![]() 與
與![]() 軸交于點(diǎn)
軸交于點(diǎn)![]() ,交
,交![]() 軸于點(diǎn)
軸于點(diǎn)![]() ,直線
,直線![]() 與
與![]() 關(guān)于
關(guān)于![]() 軸對(duì)稱,交
軸對(duì)稱,交![]() 軸于點(diǎn)
軸于點(diǎn)![]() ,
,
(1)求直線![]() 的解析式;
的解析式;
(2)過(guò)點(diǎn)![]() 在
在![]() 外作直線
外作直線![]() ,過(guò)
,過(guò)![]() 點(diǎn)作
點(diǎn)作![]() 于點(diǎn)
于點(diǎn)![]() ,過(guò)
,過(guò)![]() 點(diǎn)作
點(diǎn)作![]() 于點(diǎn)
于點(diǎn) ![]() .求證:
.求證:![]()
(3)如圖2,如果![]() 沿
沿![]() 軸向右平移,
軸向右平移,![]() 邊交
邊交![]() 軸于點(diǎn)
軸于點(diǎn)![]() ,點(diǎn)
,點(diǎn)![]() 是
是![]() 的延長(zhǎng)線上的一點(diǎn),且
的延長(zhǎng)線上的一點(diǎn),且![]() ,
,![]() 與
與![]() 軸交于點(diǎn)
軸交于點(diǎn)![]() ,在
,在![]() 平移的過(guò)程中,
平移的過(guò)程中,![]() 的長(zhǎng)度是否為定值,請(qǐng)說(shuō)明理由.
的長(zhǎng)度是否為定值,請(qǐng)說(shuō)明理由.

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】某市為創(chuàng)建全國(guó)文明城市,開展“美化綠化城市”活動(dòng),計(jì)劃經(jīng)過(guò)若干年使城區(qū)綠化總面積新增360萬(wàn)平方米.自2013年初開始實(shí)施后,實(shí)際每年綠化面積是原計(jì)劃的1.6倍,這樣可提前4年完成任務(wù).
(1)問(wèn)實(shí)際每年綠化面積多少萬(wàn)平方米?
(2)為加大創(chuàng)城力度,市政府決定從2016年起加快綠化速度,要求不超過(guò)2年完成,那么實(shí)際平均每年綠化面積至少還要增加多少萬(wàn)平方米?
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖1所示,邊長(zhǎng)為a的正方形中有一個(gè)邊長(zhǎng)為b的小正方形,如圖2所示是由圖1中陰影部分拼成的一個(gè)正方形.
(1)設(shè)圖1中陰影部分面積為S1,圖2中陰影部分面積為S2.請(qǐng)直接用含a,b的代數(shù)式表示S1,S2;
(2)請(qǐng)寫出上述過(guò)程所揭示的乘法公式;
(3)試?yán)眠@個(gè)公式計(jì)算:(2+1)(22+1)(24+1)(28+1)+1.

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】某化工車間發(fā)生有害氣體泄漏,從泄漏開始到完全控制利用了![]() ,之后將對(duì)泄漏的有害氣體進(jìn)行處理,線段
,之后將對(duì)泄漏的有害氣體進(jìn)行處理,線段![]() 表示氣體泄漏時(shí)車間內(nèi)檢測(cè)表顯示數(shù)據(jù)
表示氣體泄漏時(shí)車間內(nèi)檢測(cè)表顯示數(shù)據(jù)![]() 與時(shí)間
與時(shí)間![]() (
(![]() ) 之間的函數(shù)關(guān)系(
) 之間的函數(shù)關(guān)系(![]() ), 反比例函數(shù)
), 反比例函數(shù)![]() 對(duì)應(yīng)曲線
對(duì)應(yīng)曲線![]() 表示氣體泄漏控制后檢測(cè)表顯示數(shù)據(jù)
表示氣體泄漏控制后檢測(cè)表顯示數(shù)據(jù)![]() 與時(shí)間
與時(shí)間![]() (
(![]() ) 之間的函數(shù)關(guān)系(
) 之間的函數(shù)關(guān)系(![]() ).根據(jù)圖像解答下列問(wèn)題:
).根據(jù)圖像解答下列問(wèn)題:
(1)試求出檢測(cè)表在氣體泄漏之初顯示的數(shù)據(jù)(即點(diǎn)![]() 的縱坐標(biāo));
的縱坐標(biāo));
(2)求反比例函數(shù)![]() 的表達(dá)式, 并確定車間內(nèi)檢測(cè)表恢復(fù)到氣體泄漏之初數(shù)據(jù)時(shí)對(duì)應(yīng)
的表達(dá)式, 并確定車間內(nèi)檢測(cè)表恢復(fù)到氣體泄漏之初數(shù)據(jù)時(shí)對(duì)應(yīng)![]() 的值.
的值.

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖:一把直尺壓住射線OB,另一把直尺壓住射線OA并且與第一把直尺交于點(diǎn)P,小明說(shuō):“射線OP就是∠BOA的角平分線.”他這樣做的依據(jù)是( )
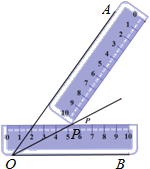
A.角平分線上的點(diǎn)到這個(gè)角兩邊的距離相等
B.角的內(nèi)部到角的兩邊的距離相等的點(diǎn)在角的平分線上
C.三角形三條角平分線的交點(diǎn)到三條邊的距離相等
D.以上均不正確
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】為了更好改善河流的水質(zhì),治污公司決定購(gòu)買10臺(tái)污水處理設(shè)備![]() 現(xiàn)有A,B兩種型號(hào)的設(shè)備,其中每臺(tái)的價(jià)格,月處理污水量如下表:經(jīng)調(diào)查:購(gòu)買一臺(tái)A型設(shè)備比購(gòu)買一臺(tái)B型設(shè)備多2萬(wàn)元,購(gòu)買2臺(tái)A型設(shè)備比購(gòu)買3臺(tái)B型設(shè)備少6萬(wàn)元.
現(xiàn)有A,B兩種型號(hào)的設(shè)備,其中每臺(tái)的價(jià)格,月處理污水量如下表:經(jīng)調(diào)查:購(gòu)買一臺(tái)A型設(shè)備比購(gòu)買一臺(tái)B型設(shè)備多2萬(wàn)元,購(gòu)買2臺(tái)A型設(shè)備比購(gòu)買3臺(tái)B型設(shè)備少6萬(wàn)元.
A型 | B型 | |
價(jià)格 | a | b |
處理污水量 | 240 | 200 |
![]() 求a,b的值;
求a,b的值;
![]() 治污公司經(jīng)預(yù)算購(gòu)買污水處理設(shè)備的資金不超過(guò)105萬(wàn)元,你認(rèn)為該公司有哪幾種購(gòu)買方案;
治污公司經(jīng)預(yù)算購(gòu)買污水處理設(shè)備的資金不超過(guò)105萬(wàn)元,你認(rèn)為該公司有哪幾種購(gòu)買方案;
![]() 在
在![]() 的條件下,若每月要求處理污水量不低于2040噸,為了節(jié)約資金,請(qǐng)你為治污公司設(shè)計(jì)一種最省錢的購(gòu)買方案.
的條件下,若每月要求處理污水量不低于2040噸,為了節(jié)約資金,請(qǐng)你為治污公司設(shè)計(jì)一種最省錢的購(gòu)買方案.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com