
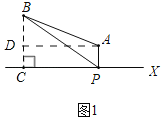
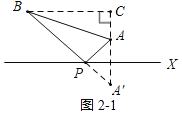
【題目】著名的恩施大峽谷(A)和世界級自然保護區星斗山(B)位于筆直的滬渝高速公路X同側,AB=50km,A、B到直線X的距離分別為10km和40km,要在滬渝高速公路旁修建一服務區P,向A、B兩景區運送游客.小民設計了兩種方案,圖1是方案一的示意圖(AP與直線X垂直,垂足為P),P到A、B的距離之和S1=PA+PB,圖2是方案二的示意圖(點A關于直線X的對稱點是A',連接BA′交直線X于點P),P到A、B的距離之和S2=PA+PB

(1)S1=_____km.S2=_____km.
(2)PA+PB的最小值為_____km.
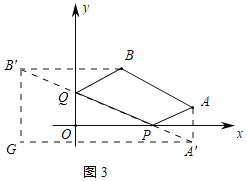
(3)擬建的恩施到張家界高速公路與滬渝高速公路垂直,建立如圖3所示的直角坐標系,B到直線的距為30km,請你在X旁和P旁各修建一服務區P、Q,使P、A、B、Q組成的四邊形的周長最小,(用尺畫出點P和點Q的位置)這個最小值為_____km.
【答案】(40![]() +10)
+10) ![]()
![]() (50+50
(50+50![]() ).
).
【解析】
(1)根據勾股定理分別求得S1、S2的值即可;
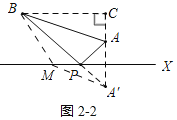
(2)在公路上任找一點M,連接MA,MB,MA',由軸對稱知MA=MA,由三角形的三邊關系得出MB+MA=MB+MA'>A'B,得出S2=BA'為最小;
(3)過A作關于x軸的對稱點A',過B作關于y軸的對稱點B',連接A'B',交x軸于點P,交y軸于點Q,求出A'B'的值即可.在公路上任找一點M,連接MA,MB,MA',由軸對稱知MA=MA,由三角形三邊關系得出MB+MA=MB+MA'>A'B,S2=BA'為最小;即可得出答案.
解:(1)如圖1中,過B作BC⊥X于C,AD⊥BC于D,則CP=AD,
則BC=40km,
又∵AP=10,
∴BD=BC﹣CD=40﹣10=30km.
在△ABD中,AD=![]() =40(km),
=40(km),
∴CP=40km,
在Rt△PBC中,BP=![]() =
=![]() =40
=40![]() (km),
(km),
∴S1=40![]() +10(km).
+10(km).
如圖2﹣1中,過B作BC⊥AA′垂足為C,
則A′C=50km,
又∵BC=40km,
∴BA'=![]() =10
=10![]() (km),
(km),
由軸對稱知:PA=PA',
∴S2=BA'=10![]() km,
km,
故答案為:(40![]() +10),10
+10),10![]() ;
;
由軸對稱知MA=MA',
∴MB+MA=MB+MA'>A'B,
∴S2=BA'=10![]() km為最小,
km為最小,
即PA+PB的最小值為10![]() km;
km;
故答案為:10![]() ;
;
(3)過A作關于x軸的對稱點A',過B作關y軸的對稱點B',連接A'B',交x軸于點P,交y軸于點Q,如圖3所示:
則P,Q即為所求.
過A'、B'分別作x軸、y軸的平行線交于點G,
B′G=40+10=50km,A′G=30+30+40=100km,
A'B'=![]() =50
=50![]() (km),
(km),
∴AB+AP+BQ+QP=AB+A′P+PQ+B′Q=50+50![]() km,
km,
∴所求四邊形的周長為(50+50![]() )km;
)km;
故答案為:(50+50![]() ).
).


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】如圖,直線![]() 與x軸、y軸分別交于C、D兩點,與雙曲線
與x軸、y軸分別交于C、D兩點,與雙曲線![]() 在第一象限內交于點P,過點P作
在第一象限內交于點P,過點P作![]() 軸于點A,
軸于點A,![]() 軸于點B,已知
軸于點B,已知![]() 且
且![]()
![]() 直接寫出直線的解析式______,雙曲線的解析式______;
直接寫出直線的解析式______,雙曲線的解析式______;
![]() 設點Q是直線
設點Q是直線![]() 上的一點,且滿足
上的一點,且滿足![]() 的面積是
的面積是![]() 面積的2倍,請求出點Q的坐標.
面積的2倍,請求出點Q的坐標.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,點A的坐標為(2,3)且AO=BO,∠AOB=90°則點B的坐標為( )

A.(2,3)B.(-3,2)C.(-3,-2)D.(-2,3)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】M(1,a)是一次函數y=3x+2與反比例函數y=![]() 圖象的公共點,若將一次函數y=3x+2的圖象向下平移4個單位,則它與反比例函數圖象的交點坐標為_________________.
圖象的公共點,若將一次函數y=3x+2的圖象向下平移4個單位,則它與反比例函數圖象的交點坐標為_________________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商店分兩次購進![]() 兩種商品進行銷售,兩次購進同一種商品的進價相同,具體情況如下表所示:
兩種商品進行銷售,兩次購進同一種商品的進價相同,具體情況如下表所示:
購進數量(件) | 購進所需費用(元) | ||
|
| ||
第一次 | 30 | 40 | 3800 |
第二次 | 40 | 30 | 3200 |
(1) 求![]() 兩種商品每件的進價分別是多少元?
兩種商品每件的進價分別是多少元?
(2) 商場決定![]() 種商品以每件30元出售,
種商品以每件30元出售,![]() 種商品以每件100元出售.為滿足市場需求,需購進
種商品以每件100元出售.為滿足市場需求,需購進![]() 兩種商品共1000件,且
兩種商品共1000件,且![]() 種商品的數量不少于
種商品的數量不少于![]() 種商品數量的4倍,請你求出獲利最大的進貨方案,并確定最大利潤.
種商品數量的4倍,請你求出獲利最大的進貨方案,并確定最大利潤.
查看答案和解析>>
科目:初中數學 來源: 題型:
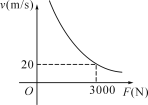
【題目】某汽車的功率P為一定值,汽車行駛時的速度v(m/s)與它所受的牽引力F(N)之間的函數關系式如圖所示.
(1)這輛汽車的功率是多少?請寫出這一函數的表達式;
(2)當它所受的牽引力為1200 N時,汽車的速度為多少千米/時?
(3)如果限定汽車的速度不超過30 m/s,則F在什么范圍內?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠C=90°,∠A=30°,取斜邊AB的中點E,易得△BCE是等邊三角形,從而得到“直角三角形中,30°角所對的直角邊等于斜邊的一半”利用這個結論解決問題:
如圖,在Rt△ABC中,∠C=90°,∠A=30°,AB=4,若動點P從點A出發,沿AB以每秒2個單位長度的速度向終點B運動.過點P作PD⊥AC于點D(點P不與點A.B重合),作∠DPQ=60°,邊PQ交射線DC于點Q.設點P的運動時間為t秒.
(1)用含t的代數式表示線段DC的長;
(2)當線段PQ的垂直平分線經過△ABC一邊中點時,直接寫出t的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC和△DEB中,已知AB=DE,還需添加兩個條件才能使△ABC≌△DEC,不能添加的一組條件是

A.BC=EC,∠B=∠E B.BC=EC,AC=DC
C.BC=DC,∠A=∠D D.∠B=∠E,∠A=∠D
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com