
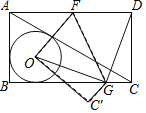
【題目】如圖,AC是矩形ABCD的對(duì)角線,⊙O是△ABC的內(nèi)切圓,現(xiàn)將矩形ABCD按如圖所示的方式折疊,使點(diǎn)D與點(diǎn)O重合,折痕為FG.點(diǎn)F,G分別在邊AD,BC上,連結(jié)OG,DG.若OG⊥DG,且⊙O的半徑長為1,則下列結(jié)論不成立的是( )
A.BC﹣AB=2B.AC=2ABC.AF=CDD.CD+DF=5
【答案】C
【解析】
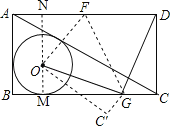
如圖,設(shè)⊙O與BC的切點(diǎn)為M,連接MO并延長MO交AD于點(diǎn)N,根據(jù)折疊的性質(zhì)得到OG=DG,根據(jù)全等三角形的性質(zhì)得到OM=GC=1,CD=GM=BC﹣BM﹣GC=BC﹣2即可判斷A;設(shè)AB=a,BC=b,AC=c,⊙O的半徑為r,推出⊙O是Rt△ABC的內(nèi)切圓可得r=![]() (a+b﹣c),根據(jù)勾股定理得到BC+AB=2
(a+b﹣c),根據(jù)勾股定理得到BC+AB=2![]() +4,AC=
+4,AC=![]() =2(1+
=2(1+![]() ),即可判斷B;再設(shè)DF=x,在Rt△ONF中,FN=3+
),即可判斷B;再設(shè)DF=x,在Rt△ONF中,FN=3+![]() ﹣1﹣x,OF=x,ON=1+
﹣1﹣x,OF=x,ON=1+![]() ﹣1,由勾股定理可得x=4﹣
﹣1,由勾股定理可得x=4﹣![]() ,即可判斷D和C.
,即可判斷D和C.
解:如圖,設(shè)⊙O與BC的切點(diǎn)為M,連接MO并延長MO交AD于點(diǎn)N,
∵將矩形ABCD按如圖所示的方式折疊,使點(diǎn)D與點(diǎn)O重合,折痕為FG,
∴OG=DG,
∵OG⊥DG,
∴∠MGO+∠DGC=90°,
∵∠MOG+∠MGO=90°,
∴∠MOG=∠DGC,
在△OMG和△GCD中,
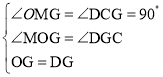 ,
,
∴△OMG≌△GCD,(AAS),
∴OM=GC=1,CD=GM=BC﹣BM﹣GC=BC﹣2.
∵AB=CD,
∴BC﹣AB=2.故A正確;
設(shè)AB=a,BC=b,AC=c,⊙O的半徑為r,
⊙O是Rt△ABC的內(nèi)切圓可得r=![]() (a+b﹣c),
(a+b﹣c),
∴c=a+b﹣2.
在Rt△ABC中,由勾股定理可得a2+b2=(a+b﹣2)2,
整理得2ab﹣4a﹣4b+4=0,
又∵BC﹣AB=2即b=2+a,代入可得2a(2+a)﹣4a﹣4(2+a)+4=0,
解得a1=1﹣![]() (舍去),a2=1+
(舍去),a2=1+![]() ,
,
∴BC+AB=2![]() +4,
+4,
∴AB=1+![]() ,BC=3+
,BC=3+![]() ,
,
∴AC=![]() =2(1+
=2(1+![]() ),
),
∴AC=2AB;故B正確;
再設(shè)DF=x,在Rt△ONF中,FN=3+![]() ﹣1﹣x=2+
﹣1﹣x=2+![]() ﹣x,OF=x,ON=1+
﹣x,OF=x,ON=1+![]() ﹣1=
﹣1=![]() ,
,
由勾股定理可得(2+![]() ﹣x)2+(
﹣x)2+(![]() )2=x2,
)2=x2,
解得x=4﹣![]() ,
,
∴CD﹣DF=![]() +1﹣(4﹣
+1﹣(4﹣![]() )=2
)=2![]() ﹣3,CD+DF=
﹣3,CD+DF=![]() +1+4﹣
+1+4﹣![]() =5,故D正確;
=5,故D正確;
∴AF=AD﹣DF=2![]() ﹣1,
﹣1,
∴AF≠CD,故C錯(cuò)誤;
故選:C.


 新課標(biāo)階梯閱讀訓(xùn)練系列答案
新課標(biāo)階梯閱讀訓(xùn)練系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,正方形ABCD中,AB=4,點(diǎn)E是BA延長線上一點(diǎn),點(diǎn)M、N分別為邊AB、BC上的點(diǎn),且AM=BN=1,連接CM、ND,過點(diǎn)M作MF∥ND與∠EAD的平分線交于點(diǎn)F,連接CF分別與AD、ND交于點(diǎn)G、H,連接MH,則下列結(jié)論正確的有( )個(gè)
①MC⊥ND;②sin∠MFC=![]() ;③(BM+DG)=AM+AG;④S△HMF=
;③(BM+DG)=AM+AG;④S△HMF=![]()
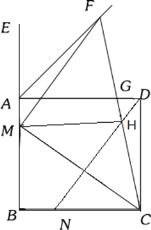
A.1B.2C.3D.4
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】已知二次函數(shù)y=x2-2![]() mx+m2+m-1(m為常數(shù)).
mx+m2+m-1(m為常數(shù)).
(1)求證:不論m為何值,該二次函數(shù)的圖像與x軸總有兩個(gè)公共點(diǎn);
(2)將該二次函數(shù)的圖像向下平移k(k>0)個(gè)單位長度,使得平移后的圖像經(jīng)過點(diǎn)(0,-2),則k的取值范圍是 .
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】國家計(jì)劃2035年前實(shí)施新能源汽車,某公司為加快新舊動(dòng)能轉(zhuǎn)換,提高公司經(jīng)濟(jì)效益,決定對(duì)近期研發(fā)出的一種新型能源產(chǎn)品進(jìn)行降價(jià)促銷.根據(jù)市場(chǎng)調(diào)查:這種新型能源產(chǎn)品銷售單價(jià)定為200元時(shí),每天可售出300個(gè);若銷售單價(jià)每降低1元,每天可多售出5個(gè).已知每個(gè)新型能源產(chǎn)品的成本為100元.
問:(1)設(shè)該產(chǎn)品的銷售單價(jià)為![]() 元,每天的利潤為
元,每天的利潤為![]() 元.則
元.則![]() _________(用含
_________(用含![]() 的代數(shù)式表示)
的代數(shù)式表示)
(2)這種新型能源產(chǎn)品降價(jià)后的銷售單價(jià)為多少元時(shí),公司每天可獲利32000元?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在Rt△ABC中,∠C=90°,以BC為直徑的⊙O交AB于點(diǎn)D,DE交AC于點(diǎn)E,且∠A=∠ADE.
(1)求證:DE是⊙O的切線;
(2)若AD=16,DE=10,求BC的長.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖1,正方形ABCD在直角坐標(biāo)系中,其中AB邊在y軸上,其余各邊均與坐標(biāo)軸平行,直線l:y=x﹣5沿y軸的正方向以每秒1個(gè)單位的速度平移,在平移的過程中,該直線被正方形ABCD的邊所截得的線段長為m,平移的時(shí)間為t(秒),m與t的函數(shù)圖象如圖2所示,則圖2中b的值為( )

A.3![]() B.5
B.5![]() C.6
C.6![]() D.10
D.10![]()
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在![]() 中,
中,![]() ,
,![]() ,點(diǎn)
,點(diǎn)![]() 是斜邊
是斜邊![]() 的中點(diǎn).點(diǎn)
的中點(diǎn).點(diǎn)![]() 從點(diǎn)
從點(diǎn)![]() 出發(fā)以
出發(fā)以![]() 的速度向點(diǎn)
的速度向點(diǎn)![]() 運(yùn)動(dòng),點(diǎn)
運(yùn)動(dòng),點(diǎn)![]() 同時(shí)從點(diǎn)
同時(shí)從點(diǎn)![]() 出發(fā)以一定的速度沿射線
出發(fā)以一定的速度沿射線![]() 方向運(yùn)動(dòng),規(guī)定當(dāng)點(diǎn)
方向運(yùn)動(dòng),規(guī)定當(dāng)點(diǎn)![]() 到終點(diǎn)
到終點(diǎn)![]() 時(shí)停止運(yùn)動(dòng).設(shè)運(yùn)動(dòng)的時(shí)間為
時(shí)停止運(yùn)動(dòng).設(shè)運(yùn)動(dòng)的時(shí)間為![]() 秒,連接
秒,連接![]() 、
、![]() .
.
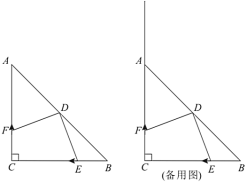
(1)填空:![]() ______
______![]() ;
;
(2)當(dāng)![]() 且點(diǎn)
且點(diǎn)![]() 運(yùn)動(dòng)的速度也是
運(yùn)動(dòng)的速度也是![]() 時(shí),求證:
時(shí),求證:![]() ;
;
(3)若動(dòng)點(diǎn)![]() 以
以![]() 的速度沿射線
的速度沿射線![]() 方向運(yùn)動(dòng),在點(diǎn)
方向運(yùn)動(dòng),在點(diǎn)![]() 、點(diǎn)
、點(diǎn)![]() 運(yùn)動(dòng)過程中,如果存在某個(gè)時(shí)間
運(yùn)動(dòng)過程中,如果存在某個(gè)時(shí)間![]() ,使得
,使得![]() 的面積是
的面積是![]() 面積的兩倍,請(qǐng)你求出時(shí)間
面積的兩倍,請(qǐng)你求出時(shí)間![]() 的值.
的值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
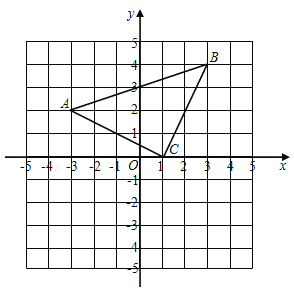
【題目】已知:△ABC在直角坐標(biāo)平面內(nèi),三個(gè)頂點(diǎn)的坐標(biāo)分別為B(3,4)、A(﹣3,2)、C(1,0),正方形網(wǎng)格中,每個(gè)小正方形的邊長是一個(gè)單位長度.
(1)畫出△ABC向下平移4個(gè)單位長度得到的△A1B1C1,點(diǎn)C1的坐標(biāo)是 ;
(2)以點(diǎn)B為位似中心,在網(wǎng)格上畫出△A2B2C2,使△A2B2C2與△ABC位似,且位似比為1:2,點(diǎn)C2的坐標(biāo)是 ;(畫出圖形)
(3)若M(a,b)為線段AC上任一點(diǎn),寫出點(diǎn)M的對(duì)應(yīng)點(diǎn)M2的坐標(biāo) .
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com