
【題目】已知,點P是正方形ABCD內的一點,連接PA、PB、PC。
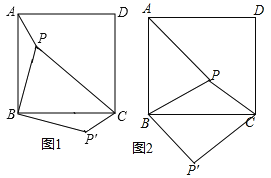
(1)將△PAB繞點B順時針旋轉90°到△P’CB的位置(如圖1)。
①設AB的長為a,PB的長為b(b<a),求△PAB旋轉到△P’CB的過程中邊PA所掃過區域的面積;
②若PA=2,PB=4,∠APB=135°,求PC的長。
(2)如圖2,在(1)的條件下,若PA2+PC2=2PB2,請說明點P必在對角線AC上。
【答案】(1)①![]() ②6;(2)將△PAB繞點B順時針旋轉90°到△P′CB的位置,由勾股逆定理證出∠
②6;(2)將△PAB繞點B順時針旋轉90°到△P′CB的位置,由勾股逆定理證出∠![]() =90°,再證∠BPC+∠APB=180°,即點P在對角線AC上.
=90°,再證∠BPC+∠APB=180°,即點P在對角線AC上.
【解析】試題分析:(1)①△PAB旋轉到△P′CB的過程中邊PA所掃過區域(圖1中陰影部分)的面積實際是大扇形OAC與小扇形BPP′的面積差,且這兩個扇形的圓心角同為90度;
②連接PP′,證△PBP′為等腰直角三角形,從而可在Rt△PP′C中,用勾股定理求得PC=6;
(2)將△PAB繞點B順時針旋轉90°到△P′CB的位置,由勾股逆定理證出∠![]() =90°,再證∠BPC+∠APB=180°,即點P在對角線AC上.
=90°,再證∠BPC+∠APB=180°,即點P在對角線AC上.
![]()
![]()
![]()
![]()
②連接PP′

根據旋轉的性質可知:
BP=BP′,∠PBP′=90°;
即:△PBP′為等腰直角三角形,
∴∠BPP′=45°,
∵∠BPA=∠BP′C=135°,∠BP′P=45°,
∴∠BPA+∠BPP′=180°,
即A、P、P′共線,
∴∠PP′C=135°-45°=90°;
在Rt△PP′C中,PP′=4![]() ,P′C=PA=2,根據勾股定理可得PC=6.
,P′C=PA=2,根據勾股定理可得PC=6.
(2)將△PAB繞點B順時針旋轉90°到△P′CB的位置,連接PP′.
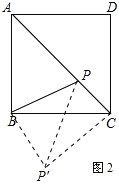
同(1)①可知:△BPP′是等腰直角三角形,即PP′2=2PB2;
∵PA2+PC2=2PB2=PP′2,
∴PC2+P′C2=PP′2,
∴∠P′CP=90°;
∵∠PBP′=∠PCP′=90°,在四邊形BPCP′中,∠BP′C+∠BPC=180°;
∵∠BPA=∠BP′C,
∴∠BPC+∠APB=180°,即點P在對角線AC上.


科目:初中數學 來源: 題型:
【題目】有A、B兩個班級,每個班級各有45名學生參加一次測驗.每名參加者可獲0,1,2,3,4,5,6,7,8,9這幾種不同的分值中的一種.測試結果A班的成績如下表所示,B班的成績如右圖所示.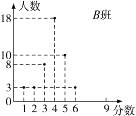
A班
分數 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
人數 | 1 | 3 | 5 | 7 | 6 | 8 | 6 | 4 | 3 | 2 |
(1)由觀察所得,班的方差大;
(2)若兩班合計共有60人及格,問參加者最少獲分才可以及格.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,邊長為a的等邊△ACB中,E是對稱軸AD上一個動點,連EC,將線段EC繞點C逆時針旋轉60°得到MC,連DM,則在點E運動過程中,DM的最小值是_____。

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(本題8分)今年我國中東部大部分地區持續出現霧霾天氣.某市記者為了了解“霧霾天氣的主要成因”,隨機調查了該市部分市民,并對調查結果進行整理,繪制了如下尚不完整的統計圖表.


請根據圖表中提供的信息解答下列問題:
(1)填空:m= ,n= ,扇形統計圖中E組所占的百分比為 %;
(2)若該市人口約有100萬人,請你估計其中持D組“觀點”的市民人數;
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com