
【題目】某自行車廠一周計劃生產150輛自行車,平均每天生產輛,由于各種原因實際每天生產量與計劃量相比有出入,下表是某周的生產情況(超產為正、減產為負):
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
增減 |
|
|
|
|
|
|
|
(1)根據記錄可知前三天共生產 輛;
(2)產量最多的一天比生產量最少的一天多生產 輛;
(3)該廠實行計劃工資制,每輛車![]() 元,超額完成任務每輛獎
元,超額完成任務每輛獎![]() 元,少生產一輛扣
元,少生產一輛扣![]() 元,那么該廠工人這一周的工資總額是多少?
元,那么該廠工人這一周的工資總額是多少?
【答案】(1)前三天共生產![]() 輛;(2)產量最多的一天比生產量最少一天多生產
輛;(2)產量最多的一天比生產量最少一天多生產![]() 輛;(3)工人這一周期的工資總額是53040元.
輛;(3)工人這一周期的工資總額是53040元.
【解析】
(1)先求出前三天增減的量,然后再加上每天的150輛,進行計算即可求解;
(2)根據增減的量的大小判斷出星期六最多,星期五最少,用多的減去少的,根據有理數的減法,減去一個數等于加上這個數的相反數進行計算即可求解;
(3)計算出這一周的增減量的總和,是正數,則超產,是負數則少生產,然后根據工資計算方法進行計算.
解:(1)![]() ,
,
![]() (輛),
(輛),
∴前三天共生產![]() 輛;
輛;
(2)觀察可知,星期六生產最多,星期五生產最少,![]() (輛),
(輛),
∴產量最多的一天比生產量最少一天多生產![]() 輛;
輛;
(3)![]() ,
,
![]()
![]()
![]()
![]()
∴工人這一周期的工資總額是:![]() (元).
(元).


 龍人圖書快樂假期暑假作業鄭州大學出版社系列答案
龍人圖書快樂假期暑假作業鄭州大學出版社系列答案科目:初中數學 來源: 題型:
【題目】如圖,Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=2cm,D為BC的中點,若動點E以1cm/s的速度從A點出發,沿著A→B→A的方向運動,設E點的運動時間為t秒(0≤t<6),連接DE,當△BDE是直角三角形時,t的值為( )

A.2B.2.5或3.5
C.3.5或4.5D.2或3.5或4.5
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下面的統計圖表示某體校射擊隊甲、乙兩名隊員射擊比賽的成績,根據統計圖中的信息,下列結論正確的是( )
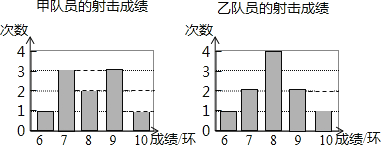
A. 甲隊員成績的平均數比乙隊員的大
B. 乙隊員成績的平均數比甲隊員的大
C. 甲隊員成績的中位數比乙隊員的大
D. 甲隊員成績的方差比乙隊員的大
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為極大地滿足人民生活的需求,豐富市場供應,某區農村溫棚設施農業迅速發展,溫棚種植面積在不斷擴大.在耕地上培成一行一行的長方形土埂,按順序間隔種植不同農作物的方法叫分壟間隔套種.科學研究表明:在塑料溫棚中分壟間隔套種高、矮不同的蔬菜和水果(同一種緊挨在一起種植不超過兩壟),可增加它們的光合作用,提高單位面積的產量和經濟效益.
現有一個種植總面積為540 m2的長方形塑料溫棚,分壟間隔套種草莓和西紅柿共24壟,種植的草莓或西紅柿單種農作物的總壟數不低于10壟,又不超過14壟(壟數為正整數),它們的占地面積、產量、利潤分別如下:
占地面積(m2/壟) | 產量(千克/壟) | 利潤(元/千克) | |
西紅柿 | 30 | 160 | 1.1 |
草莓 | 15 | 50 | 1.6 |
(1)若設草莓共種植了![]() 壟,通過計算說明共有幾種種植方案,分別是哪幾種;
壟,通過計算說明共有幾種種植方案,分別是哪幾種;
(2)在這幾種種植方案中,哪種方案獲得的利潤最大?最大利潤是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平行四邊形ABCD中,過點A作AE⊥BC,垂足為E,連接DE,F為線段DE上一點,且∠AFE=∠B.

(1)求證:△ADF∽△DEC;
(2)若AB=8,AD=![]() ,AE=6,求AF的長.
,AE=6,求AF的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某開發商進行商鋪促銷,廣告上寫著如下條款:投資者購買商鋪后,必須由開發商代租賃5年,5年期滿后由開發商以比原商鋪標價高20%的價格進行回購,投資者可在以下兩種購鋪方案中做出選擇:
方案一:按照商鋪標價一次性付清鋪款,每年可獲得的租金為商鋪標價的10%;
方案二:按商鋪標價的八折一次性付清鋪款,前3年商鋪的租金收益歸開發商所有,3年后每年可獲得的租金為商鋪標價的9%
(1)問投資者選擇哪種購鋪方案,5年后所獲得的投資收益率更高?為什么?
(注:投資收益率=![]() ×100%)
×100%)
(2)對同一標價的商鋪,甲選擇了購鋪方案一,乙選擇了購鋪方案二,那么5年后兩人獲得的收益相差7.2萬元.問甲乙兩人各投資了多少萬元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,某工廠與A,B兩地有公路、鐵路相連.這家工廠從A地購買一批每噸1000元的原料運回工廠,制成每噸8000元的產品運到B地.公路運價為1.5元(噸·千米),鐵路運價為1.2元(噸·千米),這兩次運輸共支出公路運費15000元,鐵路運費97200元.這批產品的銷售款比原料費與運輸費的和多多少元?圖中黑白相間的線表示鐵路,其它線表示公路.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,矩形OABC的頂點A、C分別在x軸和y軸上,頂點B的坐標為(n,2),點E是AB的中點,在OA上取一點D,將△BAD沿BD翻折,點A剛好落在BC邊上的F處,BD、EF交于點P
(1)直接寫出點E、F的坐標;
(2)若OD=1,求P點的坐標;
(3)動點Q從P點出發,依次經過F,y軸上的點M,x軸上的點N,然后返回到P點:
①若要使Q點運動一周的路徑最短,試確定M、N的位置;
②若n=3,求最短路徑的四邊形PFMN的周長.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com