
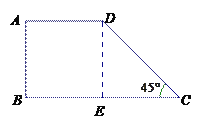
【題目】為了增強學生體質,學校鼓勵學生多參加體育鍛煉,小華同學馬上行動,每天圍繞小區進行晨跑鍛煉.該小區外圍道路近似為如圖所示四邊形ABCD,已知四邊形ABED為正方形,∠DCE=45°,AB=100米.小華某天繞該道路晨跑5圈,求小華該天晨跑的路程是多少?(結果保留整數,![]() )
)
科目:初中數學 來源: 題型:
【題目】正方形網格中(網格中的每個小正方形邊長是1),△ABC的頂點均在格點上,請在所給的直角坐標系中解答下列問題:
(1)作出△ABC繞點A逆時針旋轉90°的△AB1C1.
(2)作出△ABC關于原點O成中心對稱的△A1B2C2.
(3)請直接寫出以A1、B2、C2為頂點的平行四邊形的第四個頂點D的坐標________.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,四邊形ABCD是正方形,點E是BC邊上一動點(不與B、C重合).連接AE,過點E作EF⊥AE,交DC于點F.
(1)求證:△ABE∽△ECF;
(2)連接AF,試探究當點E在BC什么位置時,∠BAE=∠EAF,請證明你的結論.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,矩形ABCD的面積為20cm2,對角線交于點O;以AB、AO為鄰邊做平行四邊形AOC1B,對角線交于點O1;以AB、AO1為鄰邊做平行四邊形AO1C2B;…依此類推,則平行四邊形AO4C5B的面積為( )

A. ![]() cm2 B.
cm2 B. ![]() cm2 C.
cm2 C. ![]() cm2 D.
cm2 D. ![]() cm2
cm2
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知,在△ABC中,AB=AC.過A點的直線a從與邊AC重合的位置開始繞點A按順時針方向旋轉角θ,直線a交BC邊于點P(點P不與點B、點C重合),△BMN的邊MN始終在直線a上(點M在點N的上方),且BM=BN,連接CN.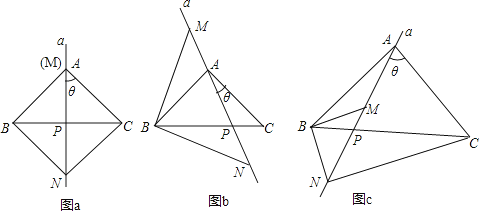
(1)當∠BAC=∠MBN=90°時,
①如圖a,當θ=45°時,∠ANC的度數為△;
②如圖b,當θ≠45°時,①中的結論是否發生變化?說明理由;
(2)如圖c,當∠BAC=∠MBN≠90°時,請直接寫出∠ANC與∠BAC之間的數量關系,不必證明.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】水果店以每箱60元新進一批蘋果共400箱,為計算總重量,從中任選30箱蘋果稱重,發現每箱蘋果重量都在10千克左右,現以10千克為標準,超過10千克的數記為正數,不足10千克的數記為負數,將稱重記錄如下:
規格 | ﹣0.2 | ﹣0.1 | 0 | 0.1 | 0.2 | 0.5 |
筐數 | 5 | 8 | 2 | 6 | 8 | 1 |
(1)求30箱蘋果的總重量
(2)若每千克蘋果的售價為10元,則賣完這批蘋果共獲利多少元
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校部分團員參加社會公益活動,準備購進一批許愿瓶進行銷售,并將所得利 潤捐助給慈善機構.根據市場調查,這種許愿瓶一段時間內的銷售量y (單位:個)與
銷售單價x(單位:元/個)之間的對應關系如圖所示: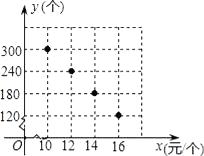
(1)y與x之間的函數關系是 .
(2)若許愿瓶的進價為6元/個,按照上述市場調查的銷售規律,求銷售利潤w(單位:元)與銷售單價x(單位:元/個)之間的函數關系式;
(3)在(2)問的條件下,若許愿瓶的進貨成本不超過900元,要想獲得最大利潤,試確定這種許愿瓶的銷售單價,并求出此時的最大利潤.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com