
【題目】如圖,AB是⊙O的直徑,BC是⊙O的切線,D是⊙O上的一點,且AD∥CO. 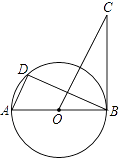
(1)求證:△ABD≌△OBC;
(2)若AB=2,BC= ![]() ,求AD的長.
,求AD的長.
【答案】
(1)證明:∵AB是⊙O的直徑,
∴∠ADB=∠90°,
∵BC是⊙O的切線,
∴∠OBC=∠90°,
∵AD∥CO,
∴∠A=∠COB,
在△ABD和△OBC中
∵∠ADB=∠OBC,∠A=∠COB,
∴△ABD∽△OCB;
(2)解:由(1)知,△ABD∽△OCB,
∴ ![]() =
= ![]() ,即AD=
,即AD= ![]() ,
,
∵AB=2,BC= ![]() ,
,
∴OB=1,
∴OC= ![]() =
= ![]() ,
,
∴AD= ![]() =
= ![]() .
.
【解析】(1)根據AB為圓O的直徑,根據圓周角定理得到∠D為90°,又BC為圓O的切線,根據切線性質得到∠CBO=90°,進而得到這兩個角相等,又AD∥CO,根據兩直線平行,得到一對同位角相等,從而利用兩角對應相等的兩三角形相似即可得證;(2)根據勾股定理求得OC= ![]() ,由(1)得到的相似三角形,根據相似三角形的對應邊成比例得出
,由(1)得到的相似三角形,根據相似三角形的對應邊成比例得出 ![]() =
= ![]() ,即AD=
,即AD= ![]() ,求出AD的長.
,求出AD的長.
【考點精析】通過靈活運用切線的性質定理,掌握切線的性質:1、經過切點垂直于這條半徑的直線是圓的切線2、經過切點垂直于切線的直線必經過圓心3、圓的切線垂直于經過切點的半徑即可以解答此題.


 奪冠訓練單元期末沖刺100分系列答案
奪冠訓練單元期末沖刺100分系列答案 新思維小冠軍100分作業本系列答案
新思維小冠軍100分作業本系列答案 名師指導一卷通系列答案
名師指導一卷通系列答案科目:初中數學 來源: 題型:
【題目】如圖,已知∠1=∠2,要得到△ABD≌△ACE,從下列條件中補選一個,則錯誤的是( )

A.AB=AC B.DB=EC C.∠ADB=∠AEC D.∠B=∠C
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下圖是交警在一個路口統計的某個時段來往車輛的車速(單位:千米/小時)情況,則下列關于車速描述錯誤的是( )
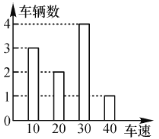
A. 平均數是23 B. 中位數是25 C. 眾數是30 D. 方差是129
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,O為坐標原點,△ABC的三個頂點坐標分別為A(-1,-2),B(1,1),C(-3,1),△A1B1C1是△ABC向下平移2個單位,向右平移3個單位得到的.
(1)寫出點A1、B1、C1的坐標,并在右圖中畫出△A1B1C1;
(2)求△A1B1C1的面積.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知PA、PB切⊙O于A,B兩點,連AB,且PA,PB的長是方程x2﹣2mx+3=0的兩根,AB=m.試求: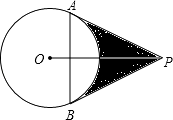
(1)⊙O的半徑;
(2)由PA,PB, ![]() 圍成圖形(即陰影部分)的面積.
圍成圖形(即陰影部分)的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,△ABC是等腰三角形,AB=AC,點D,E,F分別在AB,BC,AC邊上,且BD=CE,BE=CF.
(1)求證:△DEF是等腰三角形;
(2)猜想:當∠A滿足什么條件時,△DEF是等邊三角形?并說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,∠A=m°,∠ABC和∠ACD的平分線交于點A1 , 得∠A1;∠A1BC和∠A1CD的平分線交于點A2 , 得∠A2;…∠A2016BC和∠A20l6CD的平分線交于點A2017 , 則∠A2017=°. 
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖①,在平面直角坐標中,邊長為2的正方形OABC的兩頂點A,C分別在y軸、x軸的正半軸上,O為坐標原點.現將正方形OABC繞O點順時針旋轉,當A點第一次落在直線y=x上時停止旋轉,旋轉過程中,AB邊交直線y=x于點M,BC邊交x軸于點N.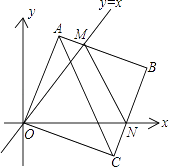
(1)當A點第一次落在直線y=x上時,求點A所經過的路線長;
(2)在旋轉過程中,當MN和AC平行時,求正方形OABC旋轉的度數;
(3)設△MBN的周長為p,在旋轉正方形OABC的過程中,p值是否有變化?請證明你的結論.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com