
【題目】如圖,AB是圓O的直徑,點C、D在圓O上,且AD平分∠CAB.過點D作AC的垂線,與AC的延長線相交于E,與AB的延長線相交于點F.
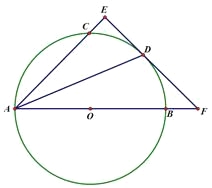
(1)求證:EF與圓O相切;
(2)若AB=6,AD=4![]()
![]() ,求EF的長.
,求EF的長.
【答案】(1)證明見解析;(2)EF=![]() .
.
【解析】
(1)連接OD,由OA=OD可得∠OAD=∠ODA,又AD平分∠BAC從而可得∠OAD=∠CAD,從而可得∠ODA=∠CAD,繼而可得OD∥AE,由EF垂直于AE,可得OD垂直于EF,從而可得EF與圓O相切;
(2)連接OD、CD、BD、BC,則CD=BD,由AB是直徑,可得∠ACB=∠ADB=90°,有勾股定理可得BD=![]() ,從而CD=2,由∠ACB=∠E可得BC∥EF,由∠OAD=∠CAD,∠ADB=∠E,可得△ADE∽△ABD,從而得
,從而CD=2,由∠ACB=∠E可得BC∥EF,由∠OAD=∠CAD,∠ADB=∠E,可得△ADE∽△ABD,從而得![]() ,可得DE=
,可得DE=![]() .
.
在Rt△CDE中,由勾股定理可得CE=![]() ,從而可得DG=
,從而可得DG=![]() .OG=3-
.OG=3-![]() .
.
在Rt△OGB中,由勾股定理可得GB=![]() ,
,
又由∠ACB=∠E,可得BC∥EF從而可得△OGB∽△ODF,得![]() ,從而可得DF=
,從而可得DF=![]() .所以EF=DE+DF=
.所以EF=DE+DF=![]()
![]()
=![]() .
.
解:(1)連接OD,∵OA=OD,∴∠OAD=∠ODA,
又∵AD平分∠BAC,∴∠OAD=∠CAD,
∴∠ODA=∠CAD,∴OD∥AE,
又∵EF垂直于AE,
∴OD垂直于EF,
∴EF與圓O相切;
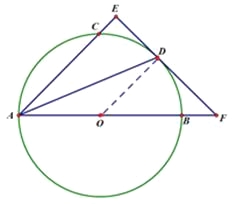
(2)連接OD、CD、BD、BC,則CD=BD,
∵AB是直徑,∴∠ACB=∠ADB=90°,
又∵AB=6,AD=4![]() ,∴BD=
,∴BD=![]() ,
,
∴CD=2,∵∠ACB=∠E,
∴BC∥EF,∵AD平分∠CAB,∴∠OAD=∠CAD,
又∵∠ADB=∠E,∴△ADE∽△ABD,
∴![]() ,即
,即![]() ,∴DE=
,∴DE=![]() .
.
在Rt△CDE中,
CE=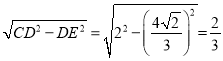
![]()
,∴DG=![]() .OG=3-
.OG=3-![]() .
.
在Rt△OGB中,GB=![]() =
= 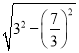 =
=![]() ,
,
∵∠ACB=∠E,∴BC∥EF.
∴△OGB∽△ODF,
∴![]() ,
,
∴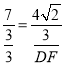 ,∴DF=
,∴DF=![]() .
.
∴EF=DE+DF=![]() +
+ ![]() =
=![]() .
.


 同步練習強化拓展系列答案
同步練習強化拓展系列答案科目:初中數學 來源: 題型:
【題目】根據規定,我市將垃圾分為了四類:可回收物、易腐垃圾、有害垃圾和其他垃圾四大類. 現有投放這四類垃圾的垃圾桶各1個,若將用不透明垃圾袋分類打包好的兩袋不同垃圾隨機投進兩個不同的垃圾桶,投放正確的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
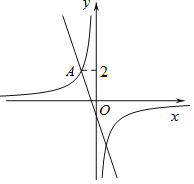
【題目】如圖,在平面直角坐標系xOy中,直線![]() 與雙曲線
與雙曲線![]() 相交于點
相交于點![]() .
.
![]() 求雙曲線
求雙曲線![]() 的表達式;
的表達式;
![]() 過動點
過動點![]() 且垂直于x軸的直線與直線
且垂直于x軸的直線與直線![]() 及雙曲線
及雙曲線![]() 的交點分別為B和C,當點B位于點C下方時,求出n的取值范圍.
的交點分別為B和C,當點B位于點C下方時,求出n的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
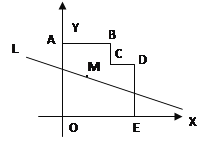
【題目】 如圖,在平面直角坐標系中,多邊形OABCDE的頂點坐標分別是O(0,0)、A(0,6)、B(4,6)、C(4,4)、D(6,4),E(6,0),若直線L經過點M(2,3),且將多邊形OABCDE分割成面積相等的兩部分,則直線L
的函數表達式是
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校為了解九年級學生的物理實驗操作情況,進行了抽樣調查.隨機抽取了40名同學進行實驗操作,成績如下:
21 | 22 | 22 | 23 | 23 | 23 | 23 | 22 | 24 | 24 |
25 | 23 | 21 | 25 | 24 | 25 | 23 | 22 | 24 | 25 |
23 | 23 | 24 | 24 | 24 | 24 | 23 | 25 | 25 | 21 |
21 | 23 | 23 | 24 | 25 | 24 | 22 | 24 | 22 | 24 |
整理上面數據,得到如下統計圖:

樣本數據的平均數、眾數、中位數如表所示:
統計量 | 平均數 | 眾數 | 中位數 |
數值 | m | 24 | 23 |
根據以上信息,解答下列問題:
(1)如表中平均數![]() 的值為_______;
的值為_______;
(2)扇形統計圖中“ 24分”部分的圓心角大小為_______度;
(3)根據樣本數據,請估計該校九年級320名學生中物理實驗操作得滿分的學生人數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在四邊形ABCD中,AB∥CD,BC⊥CD,AB=2,CD=3,在BC上取點P(P與B、C不重合)連接PA延長至E,使PA=2AE,連接PD并延長至F,使PD=3FD,以PE、PF為邊作平行四邊形,另一個頂點為G,則PG長度的最小值為_____.
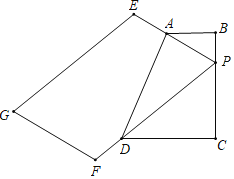
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點E是正方形ABCD中CD上的一點,把△ADE繞點A順時針旋轉90°到△ABF的位置,若四邊形AECF的面積為16,DE=1,則EF的長是( )
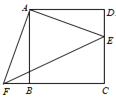
A.4B.5C.2![]() D.
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】新冠肺炎疫情爆發以來,口罩成為需求最為迫切的防護物資.在這個關鍵時刻,我國某企業利用自身優勢轉產口罩,這背后不僅體現出企業強烈的社會責任感,更是我國人民團結一心抗擊疫情的決心.據悉該企業3月份的口罩日產能已達到500萬只,預計今后數月內都將保持同樣的產能,則3月份(按31天計算)該企業生產的口罩總數量用科學記數法表示為( )
A.![]() 只B.
只B.![]() 只C.
只C.![]() 只D.
只D.![]() 只
只
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com