
【題目】如圖,AB是⊙O的直徑,弦CD⊥AB于點G,點F是CD上一點,且滿足若![]() ,連接AF并延長交⊙O于點E,連接AD、DE,若CF=2,AF=3.
,連接AF并延長交⊙O于點E,連接AD、DE,若CF=2,AF=3.
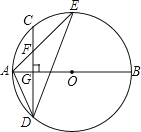
(1)求證:△ADF∽△AED;
(2)求FG的長;
(3)求tan∠E的值.
【答案】(1)證明見解析;(2)FG =2;(3) ![]() .
.
【解析】分析:(1)由AB是 O的直徑,弦CD⊥AB,根據垂徑定理可得:弧AD=弧AC,DG=CG,繼而證得△ADF∽△AED;(2)由![]() ,CF=2,可求得DF的長,繼而求得CG=DG=4,則可求得FG=2;(3)由勾股定理可求得AG的長,即可求得tan∠ADF的值,繼而求得tan∠E=
,CF=2,可求得DF的長,繼而求得CG=DG=4,則可求得FG=2;(3)由勾股定理可求得AG的長,即可求得tan∠ADF的值,繼而求得tan∠E=![]() .
.
本題解析:①∵AB是⊙O的直徑,弦CD⊥AB,
∴DG=CG,∴![]() ,∠ADF=∠AED,
,∠ADF=∠AED,
∵∠FAD=∠DAE(公共角),∴△ADF∽△AED;
②∵![]() ,CF=2,∴FD=6,∴CD=DF+CF=8,
,CF=2,∴FD=6,∴CD=DF+CF=8,
∴CG=DG=4,∴FG=CG-CF=2;
③∵AF=3,FG=2,∴AG=![]() ,
,


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
【題目】“搶紅包”是2015年春節十分火爆的一項網絡活動,某企業有4000名職工,從中隨機抽取350人,按年齡分布和對“搶紅包”所持態度情況進行了調查,并將調查結果繪成了條形統計圖和扇形統計圖.

(1)這次調查中,如果職工年齡的中位數是整數,那么這個中位數所在的年齡段是哪一段?
(2)如果把對“搶紅包”所持態度中的“經常(搶紅包)”和“偶爾(搶紅包)”統稱為“參與搶紅包”,那么這次接受調查的職工中“參與搶紅包”的人數是多少?
(3)請估計該企業“從不(搶紅包)”的人數是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,書桌上的一種新型臺歷和一塊主板AB、一個架板AC和環扣(不計寬度,記為點A)組成,其側面示意圖為△ABC,測得AC⊥BC,AB=5cm,AC=4cm,現為了書寫記事方便,須調整臺歷的擺放,移動點C至C′,當∠C′=30°時,求移動的距離即CC′的長(或用計算器計算,結果取整數,其中![]() =1.732,
=1.732, ![]() =4.583)
=4.583)

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com